Metamodeling Techniques for Multidimensional Ship Design Problems
DOI:
https://doi.org/10.25043/19098642.39Keywords:
metamodeling, kriging, radial basis functions, support vector regression, metamodel-based design optimizationAbstract
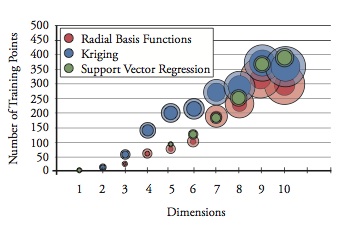
Metamodels, also known as surrogate models, can be used in place of computationally expensive simulation models to increase computational efficiency for the purposes of design optimization or design space exploration. Metamodel-based design optimization is especially advantageous for ship design problems that require either computationally expensive simulations or costly physical experiments. In this paper, three metamodeling methods are evaluated with respect to their capabilities for modeling highly nonlinear, multimodal functions with incrementally increasing numbers of independent variables. Methods analyzed include kriging, radial basis functions (RBF), and support vector regression (SVR). Each metamodeling technique is used to model a set of single-output functions with dimensionality ranging from one to ten independent variables and modality ranging from one to twenty local maxima. The number of points used to train the models is increased until a predetermined error threshold is met. Results show that each of the three methods has its own distinct advantages.Downloads
References
BOX, G. E. P. and K. B. WILSON, 1951, “On the Experimental Attainment of Optimal Conditions,” Journal of the Royal Statistical Society, Vol. 13, pp. 1-45.
CLARKE, S. M., J. H. GRIEBSCH and T. W. SIMPSON, 2005, “Analysis of Support Vector Regression for Approximation of Complex Engineering Analysis,” Journal of Mechanical Design, Vol. 127, pp. 1077-1087.
DIMOPOULOS, G. G., A. V. KOUGIOUFAS and C. A. FRANGOPOULOS, 2008, “Synthesis, Design, and Operation Optimization of a Marine Energy System,” Energy, Vol. 33, pp. 180-188.
ELY, G. R. and C. C. SEEPERSAD, 2009, "A Comparative Study of Metamodeling Techniques for Predictive Process Control of Welding Applications," ASME International Manufacturing Science and Engineering Conference, West Lafayette, Indiana, USA, Paper Number MESC2009-84189.
FANG, H., M. RAIS-ROHANI, Z. LIU and M. F. HORSTMEYER, 2005, “A Comparative Study of Metamodeling Methods for Multiobjective Crashworthiness Optimization,” Computers and Structures, Vol. 83, pp. 2121-2136.
FANG, K. T., D. K. J. LIN, P. WINKER and Y. ZHANG, 2000, “Uniform Design: Theory and Applications,” Technometrics, Vol. 42, No. 3, pp. 237-248.
FRIEDMAN, J. H., 1991, “Multivariate Adaptive Regression Splines,” The Annals of Statistics, Vol. 19, No. 1, pp. 1-67.
GIUNTA, A. and L. T. WATSON, 1998, "A Comparison of Approximation Modeling Techniques: Polynomial Versus Interpolating Models," 7th AIAA/USAF/ISSMO Symposium on Multidisciplinary Analysis & Optimization, St. Louis, MO, AIAA, Vol. 1, pp.392-404. AIAA-98-4758.
HAMMERSLEY, J. M., 1960, “Monte Carlo Methods for Solving Multivariable Problems,” Annals of the New York Academy of Sciences, Vol. 86, pp. 844-874.
HARDY, R. L., 1971, “Multiquadric Equations of Topology and Other Irregular Surfaces,” Journal of Geophysical Research, Vol. 76, No. 8, pp. 1905-1915.
HAYKIN, S., 1999, Neural Networks: A Comprehensive Foundation, Prentice Hall, Upper Saddle River, N.J.
JIN, R., W. CHEN and T. W. SIMPSON, 2001, “Comparative Studies of Metamodeling Techniques Under Multiple Modeling Criteria,” Structural and Multidisciplinary Optimization, Vol. 23, pp. 1-13.
KIM, B.-S., Y.-B. LEE and D.-H. CHOI, 2009, “Comparison Study on the Accuracy of Metamodeling Technique for Non-Convex Functions,” Journal of Mechanical Science and Technology, Vol. 23, pp. 1175-1181.
KOEHLER, J. R. and A. B. OWENS, 1996, "Computer Experiments," Handbook of Statistics, Elsevier Science, New York, Vol. 13, pp. 261-308.
LEE, Y., S. OH and D.-H. CHOI, 2008, “Design optimization Using Support Vector Regression,” Journal of Mechanical Science and Technology, Vol. 22, pp. 213-220.
MCKAY, M. D., R. J. BECKMAN and W. J. CONOVER, 1979, “A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code,” Technometrics, Vol. 21, No. 2, pp. 239-245.
MILLS, A. F., 1998, Heat Transfer, Prentice Hall, Upper Saddle River, NJ.
OWEN, A. B., 1992, “Orthogonal Arrays for Computer Experiments, Integration, and Visualization,” Statistica Sinica, Vol. 2, pp. 439-452.
PARZEN, E., 1962, “On Estimation of a Probability Density Function and Mode,” The Annals of Mathematical Statistics, Vol. 33, No. 3, pp. 1065-1076.
PERCIVAL, S., D. HENDRIX and F. NOBLESSE, 2001, “Hydrodynamic Optimization of Ship Hull forms,” Applied Ocean Research, Vol. 23, pp. 337-355.
PERI, D., M. ROSSETTI and E. F. CAMPANA, 2001, “Design Optimization of Ship Hulls via CFD Techniques,” Journal of Ship Research, Vol. 45, No. 2, pp. 140-149.
RACINE, B. J. and E. G. PATERSON, 2005, "CFD-Based Method for Simulation of Marine- Vehicle Maneuvering," 35th AIAA Fluid Dynamics Conference and Exhibit, Toronto, Ontario Canada.
SACKS, J., S. B. SCHILLER and W. J. WELCH, 1989, “Designs for Computer Experiments,” Technometrics, Vol. 31, No. 1, pp. 41-47.
SCOTT, D. W., 1992, Multivariate Density Estimation, John Wiley & Sons, Inc., New York.
SIMPSON, T., L. DENNIS and W. CHEN, 2002, “Sampling Strategies for Computer Experiments: Design and Analysis,” International Journal of Reliability and Application, Vol. 2, No. 3, pp. 209-240.
SIMPSON, T. W., T. M. MAUERY, J. J. KORTE and F. MISTREE, 1998, “Comparison of Response Surface and Kriging Models for Multidisciplinary Design Optimization,” 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Vol. 1, pp. 381-391.
VAPNIK, V., S. GOLOWICH and A. SMOLA, 1997, “Support Vector Method for Function Approximation, Regression Estimation, and Signal Processing,” Advances in Neural Information Processing Systems, Vol. 9, pp. 281-287.
WANG, X., Y. LIU and E. K. ANTONSSON, 1999, "Fitting Functions to Data in High Dimensionsal Design Space," ASME Design Engineering Technical Conferences, Las Vegas, NV, Paper Number DETC99/DAC- 8622.
WATANABE, T., T. KAWAMURA, Y. TAKEKOSHI, M. MAEDA and S. H. RHEE, 2003, "Simulation of Steady and Unsteady Cavitation on a Marine Propeller Using a RANS CFD Code," Fifth International Symposium on Cavitation, Osaka, Japan.
Published
How to Cite
Issue
Section
License
The authors who publish in this Journal certify that:
- The work submitted for publication in The Ship Science and Technology journal, was written by the author, given that its content is the product of his/her direct intellectual contribution.
- All data and references to material already published are duly identified with their respective credits and are included in the bibliographic notes and quotations highlighted as such.
- All materials submitted for publication are completely free of copyrights; consequently, the author accepts responsibility for any lawsuit or claim related with Intellectual Property Rights thereof, Exonerating of responsibility to The Science and Technology for the Development of Naval, Maritime, and Riverine Industry Corporation, COTECMAR.
- In the event that the article is chosen for publication by The Ship Science and Technology journal, the author state that he/she totally transfers reproduction rights of such to The Science and Technology for the Development of Naval, Maritime, and Riverine Industry Corporation, COTECMAR.
- The authors retain the copyright and transfer to COTECMAR the right of publication and reproduction of the work which will be simultaneously subject to the Creative Commons Attribution License (CC -BY) , which allows the license to copy, distribute, display and represent the work and to make derivative works as long as it recognizes and cites the work in the manner specified by the author or licensor.
- For more information about the Creative Commons Attribution License (CC -BY) and his use and scope, please visit the following web page https://creativecommons.org/licenses/by-sa/4.0/legalcode