Application of Cubic B-Spline Curves for Hull Meshing
DOI:
https://doi.org/10.25043/19098642.215Keywords:
cubic B-Spline curves, hull mesh, quadrilateral mesh panel, divergence theoremAbstract
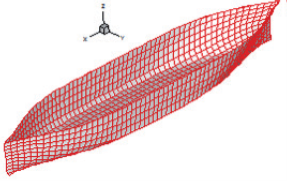
This paper describes the development of a regular hull meshing code using cubic B-Spline curves. The discretization procedure begins by the definition of B-Spline curves over stations, bow and stern contours of the hull plan lines. Thus, new knots are created applying an equal spaced subdivision procedure on defined B-spline curves. Then, over these equal transversal space knots, longitudinal B-spline curves are defined and subdivided into equally spaced knots, too. Subsequently, new transversal knots are created using the longitudinal equally spaced knots. Finally, the hull mesh is composed by quadrilateral panels formed by these new transversal and longitudinal knots. This procedure is applied in the submerged Wigley hulls Series 60 Cb=0.60. Their mesh volumes are calculated using the divergence theorem, for mesh quality evaluation.
Downloads
References
R. L. ALVAREZ and M. R. MARTINS, “Otimização das Formas de Cascos de Deslocamento em Relação a sua Resistência ao Avanço”, in XX Pan-American Conference of Naval Engineering (COPINAVAL), São Paulo, 2007.
CABRAL J., WROBEL L. and BREBBIA C., A BEM formulation using B-splines: II- multiple knots and non-uniform blending functions, Engineering Analysis with Boundary Elements. 1991, vol 7, issue 1.
CABRAL J., WROBEL L. and BREBBIA C., A BEM formulation using B-splines: I- uniform blending functions, Engineering Analysis with Boundary Elements. 1990, vol 7, issue 3.
DE BOOR C., A Practical Guide to Splines, Applied Mathematical Sciences. 2001.
J. J. JOURNEE, “Discrepancies in Hydrodynamic Coefficients of Wigley Hull Forms”, in Proceedings of the 3rd International Conference on Marine Industry (MARIND), Varna, 2001.
S. NAKAMURA, Métodos Numéricos Aplicados com Software. 1th ed. Naucalpan de Juarez, Mexico, Prentice Hall Inc, 1991.
NOWACKI H., Five Decades of Computer-Aided Ship Design, Computer-Aided Design. 2010, vol 42, pp 956-969.
R. F. RIESENFELD, “Applications of B-Spline Approximation to Geometric Problems of Computer Aided Design”, Ph.D. dissertation, Dept. of Systems and Information Science, Syracuse University, NY, 1973.
ROGERS D. F,. “B-Spline Curves and Surfaces for Ship Hull Definition”, in Symposium of Computer Aided Hull Surface Definition (SCAHD), Annapolis, MD, 1973.
C. SALHUA, “Hydrodynamic Interference between Ships with Forward Speed in Waves”, D.Sc. dissertation (in portuguese), Dept. of Naval and Ocean Engineering, Federal University of Rio de Janeiro, RJ, Brazil, 2010.
TODD F.H., Some further experiments on single-screw mechant ships forms - serie 60, SNAME Transaction, 1953.
USHATOV R., POWER H. and Rêgo SILVA J. J., Uniform bicubic B-splines applied to boundary element formulation for 3-D scalar problems, Engineering Analysis with Boundary Elements, 1994, vol 13, pp. 371-381.
VENTURA M. F., “Ship Hull Representation by Non-Uniform Rational B-Spline Surface Patches”, M.Sc. thesis, Dept. of Naval Architecture and Ocean Engineering, Glasgow, UK,1996.
YAMAGUCHI, F. A., A New Curve Fitting Method Using a CRT Computer Display, Comp. Graph and Image Processing. 1978, pp 425-437. Ship Science
Published
How to Cite
Issue
Section
License
The authors who publish in this Journal certify that:
- The work submitted for publication in The Ship Science and Technology journal, was written by the author, given that its content is the product of his/her direct intellectual contribution.
- All data and references to material already published are duly identified with their respective credits and are included in the bibliographic notes and quotations highlighted as such.
- All materials submitted for publication are completely free of copyrights; consequently, the author accepts responsibility for any lawsuit or claim related with Intellectual Property Rights thereof, Exonerating of responsibility to The Science and Technology for the Development of Naval, Maritime, and Riverine Industry Corporation, COTECMAR.
- In the event that the article is chosen for publication by The Ship Science and Technology journal, the author state that he/she totally transfers reproduction rights of such to The Science and Technology for the Development of Naval, Maritime, and Riverine Industry Corporation, COTECMAR.
- The authors retain the copyright and transfer to COTECMAR the right of publication and reproduction of the work which will be simultaneously subject to the Creative Commons Attribution License (CC -BY) , which allows the license to copy, distribute, display and represent the work and to make derivative works as long as it recognizes and cites the work in the manner specified by the author or licensor.
- For more information about the Creative Commons Attribution License (CC -BY) and his use and scope, please visit the following web page https://creativecommons.org/licenses/by-sa/4.0/legalcode