Solution to the Anti-aircraft Fire Control Problem on a Naval Platform Using the Direct Geometric Model
DOI:
https://doi.org/10.25043/19098642.110Keywords:
Fire control systems, geometric model, modelingAbstract
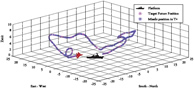
To find the kinematic model in applications different from robotics, the free-body diagram and coordinateconversion using Euler angles is frequently used. In robotics the Khalil-Kleinfinger (1986) method is used(and others), which allows coordinate conversions over several joints. In this paper a new application ofthis method to solve the fire control problem of a naval anti aircraft gun is proposed. To demonstrate theapplication a virtual model is built using Virtual Reality Modeling Language (VRML) and controlledby Matlab Simulink®. From the direct geometric model the solution of the problem is found, includingthe detection system, platform, gun and flight of the missile. This model serves as a tool for the design,testing and integration of controllers for the gun and detection system. The prediction algorithms ofthe trajectory of the target and the missile in flight models can also be integrated. The results show thatthe geometric model of complex systems with many degrees of freedom can be constructed in a precise,methodical and easy to understand manner.Downloads
References
BAO-QUAN, M. et al. Research on DynamicSimulation of Remotely-Operated WeaponStations Servo Control System. 2010 IEEEInternational Conference on IntelligentComputation Technology and Automation.China, Changsha, 2010
BERG, R.F. Estimation and prediction formanoeuvring target trajectories, IEEETransactions of Automatic Control, Vol. 28,No. 3, March 1983, pp. 294–304.
BO, B., et al. Research of Anti-aircraft GunWeapon System Simulation Platform BasedHLA and Virtools. 2011 InternationalConference on Electronics, Communicationsand Control. China, Ningbo, pp. 4455-4457,September, 2011.
CABECHINHAS, D. Integrated Solutionto Quadrotor Stabilization and AttitudeEstimation Using a Pan and Tilt Camera. 51stIEEE Conference on Decision and Control.USA, Maui, Hawaii, December, 2012.
CARTLUCCI, D. and JACOBSON, S. BallisticsTheory and Design of Guns and Ammunition.CRC Press, Taylor & Francis Group. BocaRaton, Florida, USA, 2007. ISBN: 978-1-4200-6618-0.
CELLARY W. Interactive 3D MultimediaContent, Models for Creation, Management,Search and Presentation. Department ofInformation Technology Poznan Universityof Economics. Springer. Poland. 2012. ISBN978-1-4471-2496-2.
DONGSHENG L. et al. Research on Modellingand Simulation for Pitch/Roll Two-AxisStrap-down Stabilization Platform. TheTenth International Conference on ElectronicMeasurement & Instruments. The 54thResearch Institute of CETC, Shijiazhuang,School of Instrumentation Science and OptoelectronicEngineering Beijing University ofAeronautics and Astronautics, China. 2011.
ELNASHAR, G. A mathematical model derivationof general fire control problem and solutionscenario, School of Engineering-Egyptian Armed Forces. Int. Journal of Modelling,Identification and Control, Vol. 20, No. 3,Cairo Egypt, 2013.
FOSSEN, T. Nonlinear Modelling and Control ofUnderwater Vehicles. Doctoral Thesis (PhD).Department of Engineering Cybernetics,Norwegian University of Science andTechnology. Trondheim, Norway. 1991.
FOSSEN T, Handbook of Marine CraftHydrodynamics and Motion Control, FirstEdition. Norwegian University of Science andTechnology Trondheim, Norway. John Wiley& Sons Ltd. Trondheim, Norway. 2011. ISBN:978-1-119-99149-6.
HAHN R. et al. Predictive Guidance of aMissile for Hit-to-Kill Interception. IEEETransactions on Control Systems Technology,Vol. 17, No. 4, July 2009. 1063-6536.
KHALIL, W. Y KLEINFINGER, J.F. A newgeometric notation for open and closed-looprobots. 1986 IEEE International Conferenceon Robotics and Automation, San Francisco,USA, pp. 1174-1180.
KIM D. et al. Stabilization Control for the MobileSurveillance Robot using Motion Simulator.Chungnam National University, DodaamSystems Co. International Conference onControl, Automation and Systems. Seoul,Korea. 2008.
KUMAR J. Stabilization System for CameraControl on an Unmanned Surface Vehicle.Thesis. Naval Postgraduate School. Monterey,California, USA. 2008. NSN 7540-01-280-5500.
OLLERENSHAW D. and COSTELLO M.Model of Predictive Control of a Direct-FireMissile Equipped With Canards. Oregon StateUniversity. Corvallis, Oregon, USA. 2005.
WADOO S. and KACHROO P. AutonomousUnderwater Vehicles, Modelling, ControlDesign and Simulation. CRC Press, Taylir& Francis Group. 2011. ISBN-13: 978-1439818312.
SLABAUGH G. Downloaded from: http://www.soi.city.ac.uk/~sbbh653/publications/euler.pdf. 1999.
VIVAS O. Diseño y Control de Robots IndustrialesTeoría y Práctica. Elaleph, Buenos Aires,Argentina. 2010. ISBN 978-987-1581-76-4.
WOODMAN O. An introduction to inertialNavigation, Technical report Number696, University of Cambridge, ComputerLaboratory. Cambridge UK. 2007. 37p. ISSN1476-2986.
WANG, Y., et al. Strap-down stabilization formulti-load optoelectronic imaging platform.Beihang University, Chinese Academy ofSciences. Aircraft Engineering and AerospaceTechnology: An International Journal. Beijing,China. 2012.
WEISS I. Y CROSS R. Ship Motion Effects onGun Fire Control System Design. NavalEngineers Journal, P 75-80. 1979.
YAMAKAWA S. ysflight. software flight simulator.Available on line in: http://www.ysflight.com/.Version 20090611.
ZAYED M. and BOONAERT J. An InertialSensor for Mechanical Compensation ofthe Vehicle Vertical Movement Impact onIn-Vehicle Embedded Camera Orientation.Proceedings of the 2007 IEEE IntelligentTransportation Systems Conference. Seattle,Washington, USA. 1-4244-1396-6.
Published
How to Cite
Issue
Section
License
The authors who publish in this Journal certify that:
- The work submitted for publication in The Ship Science and Technology journal, was written by the author, given that its content is the product of his/her direct intellectual contribution.
- All data and references to material already published are duly identified with their respective credits and are included in the bibliographic notes and quotations highlighted as such.
- All materials submitted for publication are completely free of copyrights; consequently, the author accepts responsibility for any lawsuit or claim related with Intellectual Property Rights thereof, Exonerating of responsibility to The Science and Technology for the Development of Naval, Maritime, and Riverine Industry Corporation, COTECMAR.
- In the event that the article is chosen for publication by The Ship Science and Technology journal, the author state that he/she totally transfers reproduction rights of such to The Science and Technology for the Development of Naval, Maritime, and Riverine Industry Corporation, COTECMAR.
- The authors retain the copyright and transfer to COTECMAR the right of publication and reproduction of the work which will be simultaneously subject to the Creative Commons Attribution License (CC -BY) , which allows the license to copy, distribute, display and represent the work and to make derivative works as long as it recognizes and cites the work in the manner specified by the author or licensor.
- For more information about the Creative Commons Attribution License (CC -BY) and his use and scope, please visit the following web page https://creativecommons.org/licenses/by-sa/4.0/legalcode