Smoothing warships movements based on wavelets

Reducción de los movimientos del buque de guerra basándose en wavelets

J.M. Riola¹
J.M. Girón²
J.J. Díaz³

Abstract

In seakeeping terminology, the Quiescent Period is known as the period of calm in rough waters to allow the ship to perform operations such as landing aircrafts and unmanned aerial vehicles (UAVs), aswell as the entry of landing crafts in the basin. Quiescence refers to the interval of time where all ship motions are within acceptable limits to perform a desired activity. Among the key issues for Quiescent Period Prediction is to be able to measure waves from a suitable distance and predict ship motions in response to waves encountered; both aspects are crucial and must be taken into account. Many of the opearations performed at sea are carried under severe weather conditions, as a result of this situation there is a need to determine this called “window of opportunity” that allows carrying them out. The paper aims to explain from the point of view of Quiescent Period Prediction, the most promising wave measurement systems, which are currently based on radar, but the main question is that if we want predictions a few seconds ahead, it will be appropriate to measure waves at a distance of some hundreds of meters, describing the new mathematical model based on wavelets in determining the spread of the waves from their initial measurement until they reach the vessel.

Key words: Quiescent Period, Wavelet, Ship Motions, Seakeeping, Control, Hydrodinamics

Resumen

Dentro del ámbito del comportamiento en la mar, se denomina Periodo Quiescente a aquellos periodos de calma que se producen en un estado de mala mar que permiten al buque llevar a cabo operaciones como pueden ser el aterrizaje de plataformas aéreas, vehículos aéreos no tripulados (UAVs) o la entrada de lanchas en el dique. El término quiescente hace referencia al intervalo de tiempo durante el cual los movimientos del buque se encuentran dentro de los límites aceptables para llevar a cabo una actividad determinada. Las claves para llegar a predecir los Periodos Quiescentes están en ser capaz de llegar a medir las olas desde una distancia adecuada, y ser capaz de llegar a predecir los movimientos que dichas olas inducirán en el buque una vez le alcance; ambos aspectos son cruciales y deberán ser tenidos en cuenta. Muchas de las operaciones que se realizan en la mar se llevan a cabo bajo condiciones climatológicas adversas, y es en estos casos donde surge la necesidad de determinar una “ventana de oportunidad” que nos permita llevarlas a cabo. El artículo trata de explicar desde el punto de vista de la predicción de periodos quiescentes los sistemas de medida de oleaje más prometedores, actualmente basados en radar, pero la inquietud principal es que si queremos una predicción de varios segundos en adelanto es necesario medir las olas a una distancia de cientos de metros, para ello se describirá el nuevo desarrollo matemático basado en “wavelets” que se ha empleado para determinar la deformación que sufren las olas desde su medida inicial hasta que alcanzan la plataforma.

Palabras claves: Periodos Quiescentes, Wavelet, Movimientos del Buque, Comportamiento en la Mar, Control, Hidrodinámica

________________________

Date Received: December 14th, 2012 - Fecha de recepción: 14 de Diciembre de 2012
Date Accepted: December 21th, 2012 - Fecha de aceptación: 21 de Diciembre de 2012

............................................................................................................................................................

¹Royal Navy of Spain. C/Arturo Soria, 289. Madrid. Spain. e-mail: jriorod@fn.mde.es
²Universidad Complutense de Madrid. Plaza Ciencias, s/n. Madrid. Spain. e-mail: gironsi@dacya.ucm.es
³Isdefe. C/Beatriz de Bobadilla, 3. Madrid. Spain. e-mail: jdiaher@oc.mde.es

Introduction

A study for Quiescent Period Prediction (QPP) seeks improved prediction of quiescent periods for wave-induced ship motions. The different reviews carried out on the research have identified several existing technologies for wave and ship motion measurement, (Riola and Girón, 2010). However, concerning shipborne instrumentation for QPP purposes only a few recent solutions are available, for instance radar.

In the current climate of reduced manning and increasingly sophisticated sub-systems in warships, tools providing guidance and assistance to operators are invaluable. During critical tasks such as aircraft operations, especially in AUVs, it may only become apparent that response limits have been exceeded when it is too late to take any action.

The ability to predict vessel motion is critically important in a large number of sectors in the shipping industry (offshore sector, float over installations, remote operator vehicle handling, helicopter landing and take off,…) where the viability of certain types of operations depend on wave-induced motions and on the need for a short quiescent period in which it is possible to safely perform an operation.

This study developed the specification for a followup project, where a technical demonstrator for quiescent period prediction was produced, and was complemented by results of sea trial off(NOT CLEAR). It essentially concerns measurement and prediction of waves (as well as ship motions), both under controlled conditions in tank tests, and in open seas to test wave measurements extracted from X-Band radar. But the main objective is the characterization and prediction of the quiescent period, via multi-resolution analysis and wavelet decomposition, expected to determine the occurrence probability of the downstream quiescent periods (ship motions) as function of the upstream quiescent period (swell measurements), whilst also calculating the distance of the measurement zone.

The navy operational requirements focus on short-term prediction for helicopter or UAV ship landing and take off. The programme is based on the theoretical application of “wavelets” in determining the spread of waves, and combines this with radar image processing and navy operational requirements. The El Pardo Hydrodynamic Ship Model Basin (CEHIPAR, for the term in Spanish) also contributes to carrying out tests with the scale model ship at its facility, the Ship Dynamics Laboratory (SDL) that provides the latest technology for wave generation and devices to measure ship motions in the presence of waves and wind. This is expected to result in the following: precise knowledge on current methods and technology for wave measurement to predict realtime ship motions due to waves and elicit military operational requirements about QPP, (Riola and Girón, 2010).

In order to obtain the experimental data for the research, a series of experiments were carried out with a scaled model in the Seakeeping Basin. It has an attached wave sensor that measures incident waves several meters before the bow seeking to emulate the effect of radar or any other measurement system capable of measuring waves at a given advance distance.

Wave Predicition

The reviews of QPP methodologies identified two types of approaches. The approach based on the ship’s past history may offer short prediction horizon (some 6-10 seconds). The approach based on distant wave measurement may offer a much longer prediction horizon (up to 2 minutes), but it is recent and requires testing.

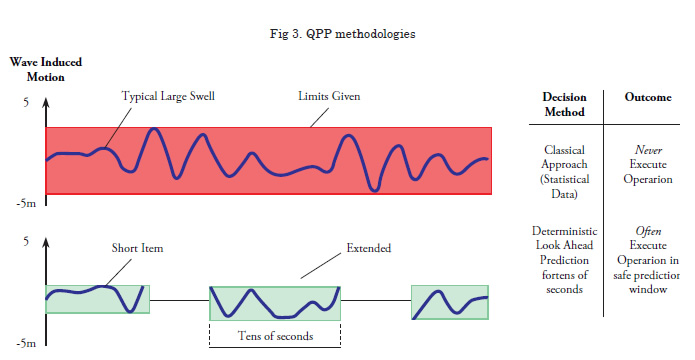
The best results of the deterministic view of seawave propagation, which allows making short-term predictions of the sea surface profile, are around 30 seconds, (Morris et al., 1997), using simulations based upon typical sea models that have shown that, under realistic conditions, accuracy above 90% prediction. This paper implies that for a large swell sea, it is realistic to expect prediction of the actual shape of the sea surface up to 30 seconds into the future with surface level prediction errors as low as 10% of the mean significant wave height. Nowadays, it is possible to know the sea surface within a range of more than 3 nautical miles by using X-Band radar. If we can process these data in time and determine the deformation of the incident wave, vessel motions from this wave elevation can be predicted. It is essential to determine the most important parameters that must be deduced as input for the wave propagation model.

(Nieto-Borge et al., 2004) proposed a method to estimate sea surface elevation maps from marine radar image sequences. This method is the extension of an existing inverse modeling technique to derive wave spectra from marine radar images, which assumes linear wave theory with temporal stationarity and spatial homogeneity of the sea surface elevation observed. (Dannenberg et al., 2009) introduced the development of a system capable of determining vessel motions two minutes ahead under mild sea states.

Ship Motion Model

Ship motions are defined by the six degrees of freedom that a ship can experience, three translations and three rotations, although methods exist for both passive and active motion stabilization used in some designs (static hull features such as skews and bilge keels, or active mechanical devices such as counterweights, anti-roll tanks, and stabilizing fins) excessive ship motions may hinder the vessel's ability to complete its mission.

In order to study the dynamic behavior of ships navigating under severe conditions, it is imperative to develop their governing equations of motion taking into account the inherent nonlinearity of large-amplitude ship motion. The following set of equations determines the basis for modelling ship motion:

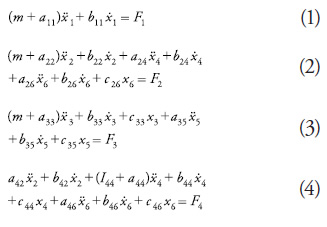
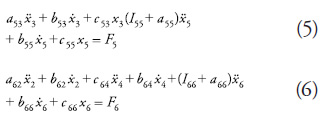
Normaly, through its complexity some movements are ignored (surge and sway) and the yaw´s effect is counteracted by the rudder´s action, so in these cases the modeling ignores certain movements because of their small size compared to other movements.

The sea state is the general condition of the free surface on a large body of water with respect to wind waves and swells at a certain location and moment. A sea state is characterized by statistics, including wave height, period, and energy spectrum. The STANAG 4194 “Standardized Wave and Wind Environments and Shipboard Reporting of Sea Conditions” adopts the 'wind sea' definition of the Douglas Sea Scale, where the use of common sources of wave and wind data for NATO Operational Areas and their application to assess operability, interoperability, and habitability characteristics of participating nation ships and establish ship designs.

The requirements taken into account for this study are included in the STANAG 4154 “Common Procedures for Seakeeping in the Ship Design Process”. This document incorporates contemporary seakeeping assessment technologies and specifies requirements for designers during the ship design cycle. It establishes common procedures for seakeeping assessment, for use in the ship design process and for future developments in supporting operational forces at sea. The limits for vertical and short takeoff and vertical landing operations specified in the document are roll 2.5º, pitch 1.5º, vertical velocity 1.0 m/sec (all of them are given in terms of root mean square amplitude). These limits are defined to permit launching and recovery of aircraft within established operational envelopes. These limits were specified for an air capable ship comparison by Comstock, (Bales and Gentile, 1982) in terms of generic criteria, which may be used as default values for any design study.

Several papers have been published regarding the quantification of the necessary prediction time to be operationally practical. (Colwell, 2004) indicated that with 6-second duration, it is possible for a helicopter to land on a ship (note that enough time should be allowed to secure the helicopter on deck). (Sherman, 2007) indicated that the anticipation must be between 8 to 10 seconds in pitch, and 20 seconds into roll.

Methodology

Measurement of sea waves can be carried out near the bow, or from a distance. The study has identified the following technologies: for shortdistance - vertical radar near the bow, ultrasonic devices; and for long-distance - radar and use of 3D fast Fourier transform.

Concerning state-of-the-art on wave measurement technology and devices, a large summary of the available theory about sea waves and their propagation is available, and the technological solutions for wave measurement are listed: buoys, vertical radar, pressure, and velocity sensors. But the most promising technologies are radar for distant waves, Light detection and ranging (LIDAR), stereo photogrammetry, and remote sensing.

Classical prediction approaches use statistical data to assess whether a task can be carried out or not. Actually, at present most ship motions are estimated through human observation. However, this may result in the outcome that an operation is never executed, although QPs do exist which have not always been correctly predicted. Our methodology, called “look forward”, is a very attractive method from a control engineering point of view, it delivers real-time wave forecasting and ship motion predictions in the relatively short term. This method requires three different tasks: 1) measurement system - the incident wave must be measured providing information about wave data, at least the significant wave height, predominant wave direction and frequency; 2) wave propagation model - to compute wave deformation along its travel to the ship, for that it is necessary to predict its propagation and its resulting deformation until it reaches the ship; 3) model of the ship dynamics - to compute all ship motions in the sailing response to the wave encountered.

Research

In order to provide an experimental basis for the research, several experiments were carried out with a scale model in a seakeeping basin with a wavemaker. The model has an attached wave sensor that measures incident waves several meters in front of the bow to emulate the effect of radar or any other measurement system capable of measuring waves from a certain distance in advance. The seakeeping laboratory has a 150 x 30 x 5-m basin equipped with a principal carriage and sub-carriages whose objective is high-precision reproduction of all possible horizontal movements along the basin against regular and irregular waves.

The method assumes that a device is taking measurements of distant waves. During the development of the method, several experimental tasks were performed, based on towing tank with wavemaker and scaled ships. The wave measurement device was emulated using a water level sensor attached at some distance from the ship. The final status reached shows QPP satisfactory results.

Wavelet analysis is becoming a common tool for analyzing localized energy variations within a time series. By decomposing a time series into time-frequency space, one is able to determine both the dominant modes of variability and how those modes vary over time. The wavelet transform has been used for numerous studies. In this research, the Fourier Transform has not been used because, although this transform identifies all spectral components present in a signal, it does not provide any information regarding the temporal (time) localization of these components. Fourier Transform is used in stationary signals where the spectral components do not change over time, so it is not necessary to know any time information. However, non-stationary signals consist of time varying spectral components and some other ways to determine time localization of spectral components must be found.

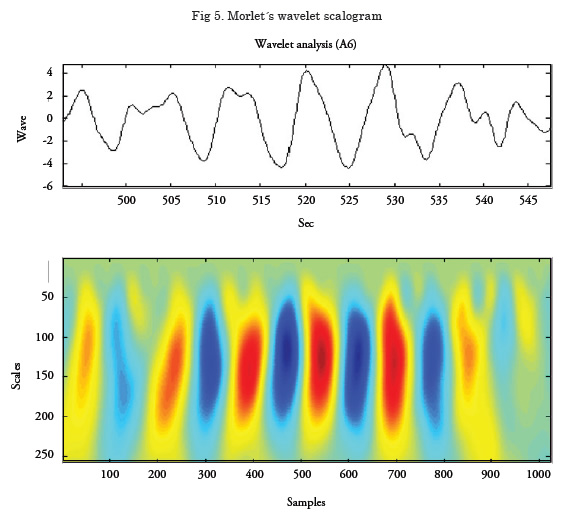
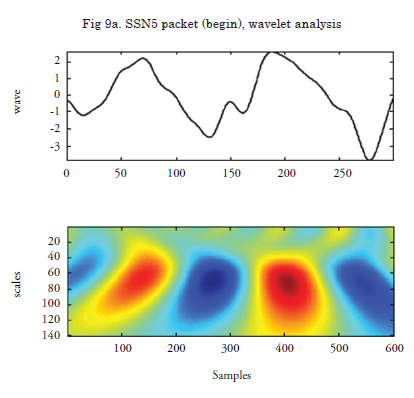
The following figure (see Fig. 5 in page 56) illustrates a wave analysis with Morlet´s wavelet and its scalogram. The fundamental idea is that the wave is changing, deforming itself over time and this information must be analysed, "photo after photo" of the deformation.

The implementation of this method requires two fundamental aspects, taking data collection and digital processing; thereby, two subsystems are necessary: the data collection subsystem and the processing unit. The data collection system allows measuring the incident wave from a distance and extracting a temporary record of the principal parameters like wave height to send them to the digital processing unit. The second subsystem can be represented in several ways (micro-controller, embedded computer, industrial computer...).

A series of experiments were performed at the SDL, where the pitch-heave-roll motions of a scaled military ship were recorded, by moving this scale vessel against irregular seas generated by the wavemaker. Data were obtained with irregular seas from SSN4 to SSN7, with Bretschneider and JONSWAP spectra. Concerning ship speed and heading, the experiments considered three speeds (18, 19, and 20 knots), and headings of 180º, 135º, 90º, 45º, and 0º. All the results were analyzed to get an idea of the occurrence of quiescent periods.

Waves were measured; our proposed QP prediction method takes data from distant waves, applies wavelets, and predicts the waves the ship will encounter. It is a method that looks forward, taking advantage of sensors like Radar or LIDAR. In our case, irregular waves were generated and their propagation was measured with several water height sensors fixed at regular distances along the basin. These experimental data constitute the basis for evaluating the performance of the QP prediction.

The main instrumentation implemented in the model at SDL was a micro-controller for the onboard system to carry out experimental tests, whose data are the baseline of the experiments and must be used to determine the kindness of the research. The model has also self-control in terms of direction and speed, to ensure greater reliability, instead of methods where the model is towed. Fig. 6 shows the onboard instrumentation.

The main data of interest obtained in SDL are listed as a set of variables: incident waves, pitch, roll, heave, and vertical accelerations in different positions, which provide different results because the ship’s center of gravity could be on the bow or on the stern flight deck. By using these experimental data, it is possible to apply the STANAG 4154 limits and graphically represent what happens. In order to study this phenomenon, we took into account the concept of minimal warning time and minimal forecast time whose definitions are: minimal warning time is the minimum advance time with which the occurrence of a QP needs to be known for the prediction to be useful. The prediction is made for a specific operation of which a “critical part” and its duration are to be known. The minimal forecast time is the sum of the minimal warning time plus the duration of the critical part of the operation and needs to be shorter than the prediction window of the QP predictor.

The following figures were the result of these experimental tests; one test is presented ahead (SSN5 sea state, heading 180º and 19 knots). These figures show the original data and the pre-processed data. The first group includes the original data obtained. As a first signal cleaning task, low-pass filtering was applied to eliminate high-frequency noise. The low-pass filtering is different for each data record. The following figures represent the pre-processed data, which was filtered to clean the high-frequency noise of the signals. A recursive Chebyshev filter was used with a Matlab filtfilt instruction to avoid inducing mismatches.

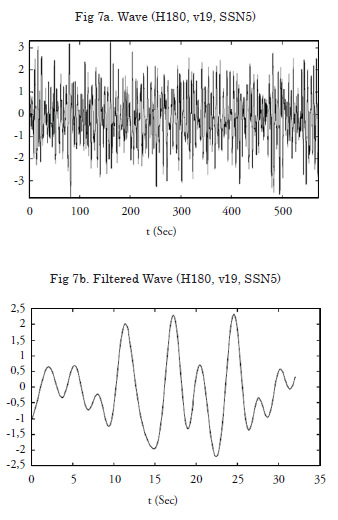
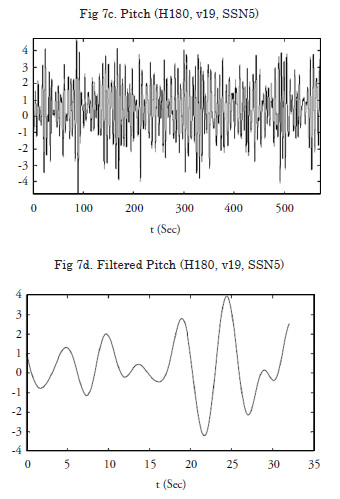
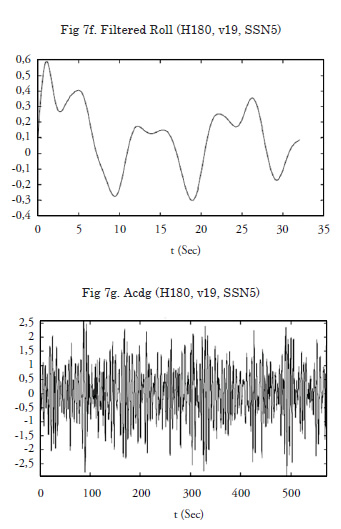
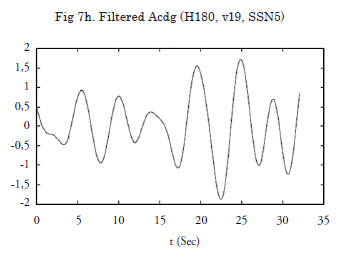
Wavelets

Extensive literature is available to explain the wavelets. If we have a signal to analyze, for example a sinusoidal signal, we select one baby wavelet, which in this case is a Gaussian wavelet, and modify this wavelet (changing two parameters: duration and time shift) until the baby wavelet matches, as closely as possible, the segment of the signal under analysis. Once this wavelet is obtained, we subtract the wavelet form the signal and try to find another baby wavelet to match the remaining signal, and so on along the specified number of iterations. The final result of the process is to have the signal decomposed into a sum of baby wavelets.

The initial mathematical position was proposed by Joseph Fourier (1807), who indicated: “An arbitrary function, continuous or with discontinuities, defined in a finite interval by an arbitrarily capricious graph can always be expressed as a sum of sinusoids”. Several publications support this stance, such as (Vetterli and Kovacevic, 2009), (Lee and Kwon paper, 2003).

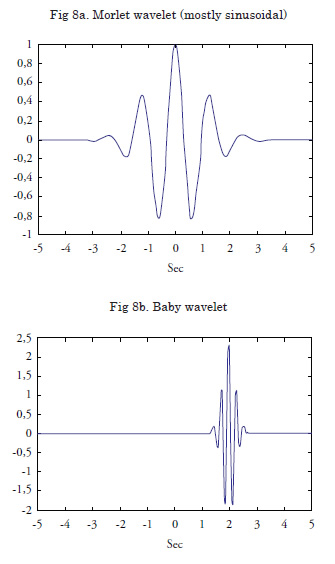
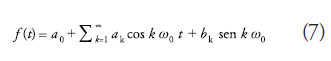
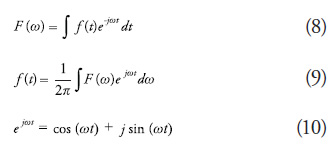
A wavelet, ψ, is a zero-average function, which is dilated with a scale parameter (s) and translated by another (u), like a windowed Fourier transform, a wavelet transform can measure the time-frequency variations of spectral components, but it has a different time-frequency resolution.

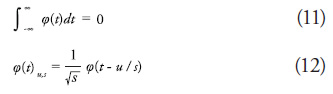
The wavelet transform can also detect and characterize transients with a zooming procedure across scales; this zooming capability not only locates isolated singular events, but can also characterize more complex multifractal signals having non-isolated singularities.

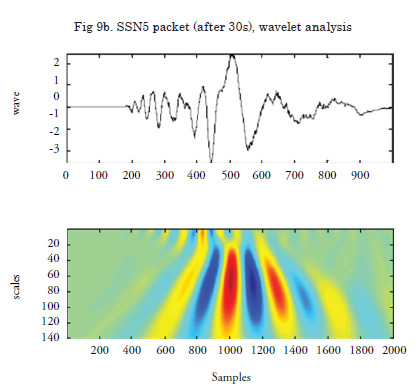
The proposal measured waves, analyzed and decomposed them into wavelets. Then the wavelets were propagated according to their own group velocity till reaching the ship. And, finally, from the propagated wavelets the wave that will reach the ship is synthesized (recovered). In summary, three steps take place: analysis, propagation, and recovery. Fig. 9 (see page 60) shows the analysis performed on a wave group under SS5 sea condition; the first is the decomposition of the measured wave into wavelets; thesecond is the subsequent analysis after the propagation, 30 seconds after the initial one, proving how the wave group spreads itself until reaching the vessel.

Conclusions

Currently, the overall decision making process is more efficient and inclusive and has speeded up; it is for this reason that the prediction of QPs is of utmost importance. The warship scenario in which we move is increasingly complex and demanding. The accelerated rythym of the growth of scientific and technological development is of great benefit but also presents a big challenge for any country. One of the reasons is the increased use of UAVs, which need to automatically land on ships. Likewise, the progressive introduction of automated tasks in sea operations demands better prediction of QPs. These appreciations are confirmed by recent NATO Science and Technolgy Organization (STO) workshops. Therefore, it is advisable to continue and extend the research on QPP. In general, computers, software tools, and electronic technology have reached a very powerful status, but this should be well exploited. On the other hand, from the experiences during the study with commercial solutions for distant wave measurements, it seems that more should be done for QPP, given that QPP is not only a matter of distant measurement, it also involves a suitable methodology for QP prediction.

While, traditionally, ship motion limits have been described in terms of maximum pitch and roll, these metrics do not fully capture the nature of ship motion and may contribute to unnecessarily restrictive boundaries. We must reinforce the idea that Dynamic Deck Motion Limits (DDMLs), based on real‐time measurements of motions can be combined with QPP technology to determine a period of acceptable motions to land helicopters or UAVs. In summary, two main challenges exist for future research: distant wave measurement and QPP methods.

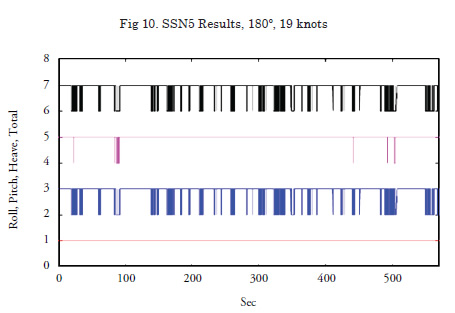
Because the starting instant of the “operational window of opportunity” has to be known sufficiently in advance, it is necessary to include the minimal warning time and the duration of the critical operation itself. As result of the experiments, a final figure was made for each. It shows four records: one record for roll, one for pitch, one for heave, and the fourth is the combination of the other three records and represents when there is a QP according to STANAG 4156. Fig. 10 (see page 61) shows a “1” level meaning when we achieve the objectives and a “0” when these are not acheived.

The combination of three ones yields another one and its translation is a QP. Then we must analyze when these QPs have enough advance time to become an operational window of opportunity.

As a result of research, we can state that as the intensity level of the sea increases, the number of quiescent periods is consistently lower. Also, we can safely assume that the great majority of QPs, with the procedure already described, have been identified, with the propagation method based on wavelets also being a resounding success. We must stress that the best conditions studied were an SSN4 sea state and 0° heading in which case we are talking about a constant QP, and obviously under the most adverse conditions with SSN7 many QPs were determined with enough quality to allow for different onboard operations, as it is also shown by STANAG.

For that reason, we focused our research to ensure that relevant knowledge and technology are available and that they are subjected to analysis by using the best possible methods to be taken into account in warship operation activities like: ramp clearance during landing operations; helicopter landing/take-off or pickup/delivery operations during VERTREP or sling operations; launch/ recovery of manned crafts - operation of deployment and retrieval of small crafts with hoisting gear; launch/recovery of unmanned vehicles (UAV, USV or UUV); launch and recovery of remote operated vehicles (ROV) or rigid inflatable boats (RIB); cable tensioning during abeam replenishment at sea; launch/recovery of towed sonar; general handling, traverse or maintenance and repair activities; firing operations; etc.

References

COLWELL, J.L. (2002). Maritime Helicopter Ship Motion Criteria - Challenges for Operational Guidance. Challenges for Operational Guidance - NATO RTO Systems Concepts and Integration Panel SCI-120. Berlin, Germany.

COLWELL, J.L. (2004). Flight Deck Motion System (FMDS): Operating Concepts and System Description. Defence R&D Canada, Technical Memorandum, DRDC Atlantic TM 2004-003.

COMSTOCK, E., BALES, S., AND GENTILE, D. (1982). Seakeeping Performance Comparison of Air Capable Ships. Naval Engineers Journal, 94 (2), 101–117.

DANNENBERG, J., REICHERT, K. AND VAN DEN BOOM, H. (2009). Wave Profiles Derived from Nautical X-band Radar as Data Source for Ship Motion Prediction. 11th International Workshop on Wave Hindcasting & Forecasting. Halifax, Canada.

FERNÁNDEZ, A. (2007). Estudio de Técnicas Basadas en la Transformada Wavelet y Optimización de sus Parámetros para la Clasificación por Texturas de Imágenes Digitales. Tesis. Universidad Politécnica de Valencia.

LEE, H.S. AND KWON, S.H. (2003). Wave Profile Measurement by Wavelet Transform. Ocean Engineering, 30, 2313-2328.

MORRIS, E.L., ZIENKIEWICZ, H.K. AND BELMONT, M.R. (1997). Shortterm Forecasting of the Sea Surface Shape. International Shipbuilding Progress, vol 45, 444, 383-400.

NIETO-BORGE, J., RODRIGUEZ, G., HESSNER, K. AND IZQUIERDO, P. (2004). Inversion of Marine Radar Images for Surface Wave Analysis. J. Atmospheric Ocean Technology, 21, 1291-1300.

RIOLA, J.M. AND GIRÓN-SIERRA, J.M. (2010). Quiescent Period Prediction. Boletín de Observación Tecnológica en Defensa, 27, 21-23.

RIOLA, J.M. AND DÍAZ, J.J. (2010). Predicción de Periodos Quiescentes. 49º Congreso de Ingeniería Naval e Industria Marítima. Bilbao, Spain.

RIOLA, J.M. AND DÍAZ, J.J. (2011). Quiescent Period Prediction. Specialists Meeting AVT– 170 on Active Suspension Technologies for Military Vehicles and Platforms – Applied Vehicle Technology Panel (AVT) – Research and Technology Organization (RTO) – NATO. Sofia, Bulgaria.

RIOLA, J.M., DÍAZ, J.J. AND GIRÓNSIERRA, J.M. (2011). The prediction of calm opportunities for landing on a ship: Aspects of the problem. OCEANS, 2011 IEEE - Spain, vol., no., pp.1.8, 6-9.

SHERMAN, B.W. (2007). The Examination and Evaluation of Dynamic Ship Quiescence Prediction and Detection Methods for Application in the Ship-Helicopter Dynamic Interface. Master's Thesis. Virginia Polytechnic Institute and State University.

VETTERLI, M. AND KOVACEVIC, J. (1995). Wavelets and Subband Coding. Englewood Cliffs, NJ: Prentice Hall Signal Processing Series.