
Analysis and Prediction of Welding Distortion in complex Structures Using Elastic Finite Element Method
Análisis y Predicción de Distorsiones en Estructuras Soldadas por medio de un Análisis Elástico de Elementos Finitos
Adán Vega Sáenz1
Carlos Plazaola2
Ilka Banfield2
Sherif Rashed3
Hidekazu Murakawa3
Abstract
The Elastic Finite Element Method based on the inherent strain theory is used to predict the welding distortion of ship structures. In addition, a method to predict welding distortion of complex structures by using elastic FEM is presented. To evaluate the effectiveness of the proposed method, a typical case of a ship's structure is examined and the resulting welding distortion is compared to that obtained by using thermal elastic-plastic finite element method.
Key words: Complex Ship Structures, Elastic Analysis, Finite Element Analysis, Inherent Strain, Welding Distortion.
Resumen
Un análisis elástico de elementos finitos basado en la teoría de la deformación unitaria inherente es utilizado para predecir la distorsión causada por la soldadura en estructuras de barcos. Adicionalmente, se propone un nuevo método para predecir la distorsión de estructuras complejas. Los resultados obtenidos son luego comparados con aquellos obtenidos por medio de análisis termo-plástico de elementos finitos.
Palabras claves: Análisis de Elementos Finitos, Análisis Elástico, Deformación Unitaria Inherente, Distorsión de Juntas Soldadas, Estructuras de Barcos complejas.
Date Received: November 9th, 2010 - Fecha de recepción: 9 de Noviembre de 2010
Date Accepted: January 16th, 2012 - Fecha de aceptación: 16 de Enero de 2012
________________________
1Miembro del Sistema Nacional de Investigación SNI (SENACYT). Laboratorio Especializado en Procesos de Union y Manufactura
(LEPUM), School of Mechanical Engineering, Technological University of Panama. Panamá City, Panamá. e-mail: adan.vega@utp.ac.pa
2Laboratorio Especializado en Procesos de Union y Manufactura (LEPUM), School of Mechanical Engineering, Technological University
of Panama, 0819-07289, Panamá City, Panamá. e-mails: carlos.plazaola@utp.ac.pa, ilka.banfield@utp.ac.pa
3Joining and Welding Research Institute, Osaka University, 11-1, Mihogaoka, Ibaraki, Osaka, Japan. e-mails: sherif-rashed@hcc5.bai.ne.jp
murakawa@jwri.osaka-u.ac.jp
............................................................................................................................................................
Introduction
Welding deformation is a common and important problem in industry. In recent decades, researchers have made efforts to predict and control welding deformation. There are usually three ways to determine the welding deformation: 1) experiential formulas, 2) Thermal elastic-plastic Finite Element Method (FEM), 3) Inherent strain method based on FEM (Liu, C and Zhang, X. 2009), (Wahab, M. et al., 2006).
Experiential formulas are only fit for simple shape structures. The current thermal elastic-plastic method is usually simulated in either small or simple structures like butt-jointed plates, or focuses on the local weld zones of large structures without considering the surrounding structure. For three-dimensional large structures, predicting the welding deformation by using this method is almost impossible given the requirements of calculating time and large capacity computer memory.
Compared to the thermal elastic-plastic method, the inherent strain method is an economic and simple method in the prediction of large structure welding deformation. It only requires elastic FEM analysis to predict welding deformation (Deng, D. et al., 2007). Inherent strains are the residual plastic strains caused in welding processes. They always exist in the welds and nearby where structures undergo large thermal cycles and are considered a source causing the welding deformations. The key to using this method lies in knowing the inherent strains in advance during welding deformation analysis (Liang, W. 2007).
In this paper, the inherent strains method is used to predict the welding deformation of large complex ship structures. At first, a simple example on the welding deformation of a T-joint with two fillet welds is given, and then the inherent strain method is applied to the welding deformation analysis of the large complex ship structure. After that, and based on a new method to predict welding distortion by using the inherent strain method, the welding distortion of large complex ship structures is predicted. The analysis method and results can be taken as references not only for the choices of weld sequence, welding parameters, and location of fixture, but also for prediction of welding deformation of other ship structures.
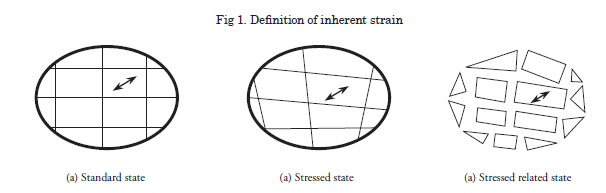
Definition of Inherent Strain
Let us consider a continuous body in different states, as shown in Fig. 1 (a), (b), and (c), respectively (Nishikawa, H. et al., 2004). State (a) is the initial stress-free state in which neither external forces nor internal stresses exist. This state is regarded as the standard state. State (b) is a residual stress state. State (c) is the stress released state in which the body is cut into small elements. From state (b) to state (c), each element deforms elastically as much as necessary to completely release the residual stress. Now, denoting the distance between two close particles in the body in the initial state (a) by ds0, and this distance in residual stress state (b) and in residual stress released state (c) by ds and ds*, respectively, the strain in state (b) and (c) can be defined by the small deformation theory as follows (Murakawa, H. 2007):

Likewise, the strain increment between state (b) and (c) can be defined as follows:
![]()
The strain in Equation 1 is usually called total strain and it satisfies compatibility conditions. The strain in Equation 2 is the inherent strain, which is incompatible. The strain in Equation 3 is elastic strain. From these equations, it may be seen that the total strain is composed of elastic and inherent strains, shown as follows:
![]()
Given that the total strain ɛ corresponds to the deformation and the elastic strain ɛe corresponds to the stress, the above equation can be written as follows:
![]()
Here, it is seen that the inherent strain produces both the deformation (inherent deformation) and the residual stress.
Inherent strain due to welding
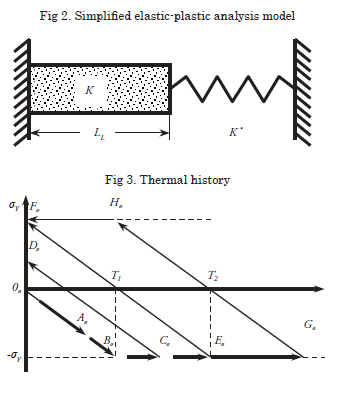
The process under which the inherent strain is produced can be modeled by using an elastically restraint bar under thermal cycle, as shown in Fig. 2 (Nishikawa, H. et al., 2004). The heating region in welding, where the inherent strain occurs, can be modeled as a bar and the adjacent region, which resists deformations, can be modeled as a spring. The bar typically experiences thermal history according to the temperature change, while the spring experiences little change in temperature, but rather acts as a restraint on the bar.
The evolution of the inherent strain according to the temperature change of the bar is explained as follows: when the bar is heated to Tmax from room temperature (zero degree) and then cooled to room temperature, compressive thermal stress is first produced in the heating process, as shown in Fig. 3. The phenomenon changes with the value of the maximum temperature, Tmax, relative to T1 and T2, which are defined as:
![]()
Where, T2 = 2T1, E is Young's modulus, σY is the yield stress, α is the thermal expansion coefficient, and β is the constraint parameter defined by using the stiffness of the bar and the stiffness of the spring as follows:
![]()
Where, k = AE/L (stiffness of bar), k* is the stiffness of spring, A is the cross-sectional area of the bar, and L is the length of the bar.
When Tmax < T1, the thermal stress does not reach the compressive yield stress in the heating process. Thus, no plastic strain (inherent strain) is produced. Because there is no inherent strain, no residual stress nor residual deformation is produced (route 0-A-0 in Fig. 3).
When T1 < Tmax < T2, the thermal stress reaches the yield stress and compressive inherent strain is produced. However, the behavior of the bar is elastic in the cooling process (route 0-B-C-D in Fig. 3.
The inherent strain ɛ*, residual stress σR and the residual deformation δR in this case are:
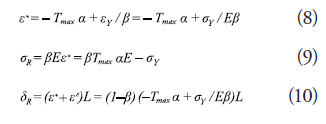
When Tmax > T2, plastic deformation takes place in both the heating and the cooling processes (route 0-B-G-H-F in Fig. 3). In this case,
It may be seen that the inherent strain, residual stress, and the residual deformation are strongly influenced by both the highest temperature, Tmax, and the constraint parameter β.
Prediction of welding distortion using Inherent Strain Method
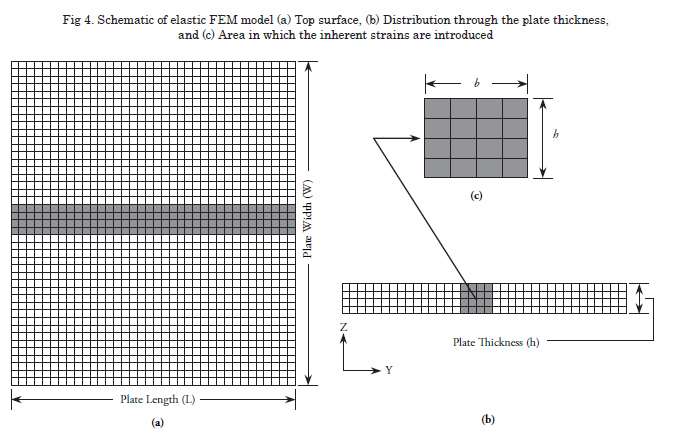
An in-house 3-D thermal-elastic-plastic solid finite element code (Serizawa, H. et al., 2007) is employed to study the relation between the inherent strain and the final distortion of the structure. Figure 4 shows an example of the FE model and the area in which the inherent strains are introduced. The simulation procedure consists of two steps:
First, the components of inherent strain produced by single pass welding are obtained through thermal-elastic-plastic finite element analysis.
Second, these inherent strain components are introduced into the elastic FEM as initial strains and the welding distortion is estimated through elastic FE analysis. To simplify the analysis, uniform distribution of inherent strains is assumed at the central region of the plate; while at both edges, average values of inherent strains are used.
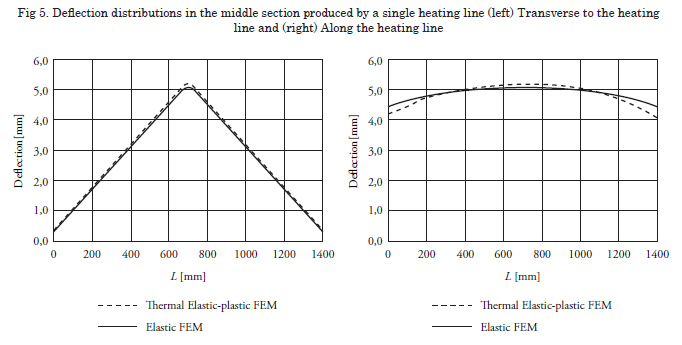
The deflections computed by the thermal-elasticplastic FEM and the elastic FEM are compared in Fig. 5. The deflection along the transverse section at the center and that along the heating line are shown in these figures. As it may be observed from these figures, the welding distortion computed by the thermal-elastic-plastic analysis is accurately reproduced by the elastic analysis. This suggests that the elastic FEM can be employed to predict the welding distortion if the inherent deformation is know in advance.
Improved method to predict welding distortion of complex ship structures by using elastic FEM
In the previous section, it was demonstrated that welding distortion can be accurately predicted by elastic FEM if the inherent strains are known. However, in shipbuilding, complex welded structures are usually found. In those cases, the welding distortion is difficult to obtain even with elastic analysis because of the influence of previous welding pass on further pass and other effects. In order to consider these influences in the analysis of plate distortion, the following procedure is proposed:
Step 1: Predict the four components of inherent
strain at the central region of the plate.
Step 2: Predict the four components of inherent
strain at plate edges.
Step 3: Correct the values obtained in Steps-1
and 2 for location of welding and plate size.
Step 4: Based on the sequence of welding,
identify if multi-passes, parallel welding, and/or crossed welding are needed. Then, obtain the correction values from databases.
Step 5: Introduce the correction values obtained in Step-4 into the values of inherent strain predicted in Step-1 to Step-3.
Step 6: Introduce the inherent strain obtained in Step-5 into the elastic FE model. n
Step 7: Repeat Steps-1 to 6 for each additional welding pass.
Step 8: Perform elastic FE analysis.
Application of proposed method to predict welding distortion of complex ship structures
To evaluate the effectiveness of the proposed method, two cases were evaluated. First, a typical transversal section of a Car Carrier ship is taken as an example. Fig. 6 shows the general arraignment of the structure. Fig. 7 shows the FE mesh model used to evaluate the welding distortion. In order to apply the procedure explained in the previous section to this case, the welding inherent strain is obtained through thermal elastic plastic analysis. The mesh model used is shown in Fig. 8. By using this model, an inherent strain database wass developed (for more details see Liang, W. et al., 2004 and Murakawa, H. et al., 2005). Later, the inherent strain from the database was introduced in the welding areas of the target structure (Fig. 7) and elastic FEM was performed.
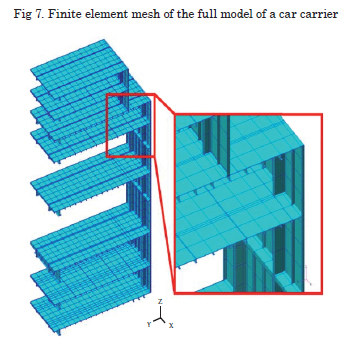
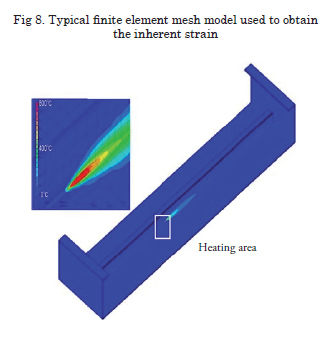
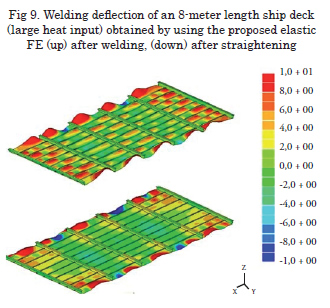
Fig. 9 shows an example of the predicted welding distortion of an 8-m length of deck section after welding and after straightening the deformed plate. In this case, the model consists of nine longitudinal fillet welds and six transverse fillet welds. Using thermal elastic plastic FE simulation, even with the faster computer, the computational time necessary to obtain similar results, is too long. Actually, not commercial software is designed to simulate such structure due to the fact that the advantage of FEM over other methods tends to disappear, once computational requirement and time exceeds designer’s plans.
As seen in Fig. 9, both welding distortion and the straightened plate can be easily obtained through this elastic FEM. The comparison with thermal elastic plastic FEM and with the experiment will be presented in future papers; however, it was found that the deviation from the experiment is less than 8%.
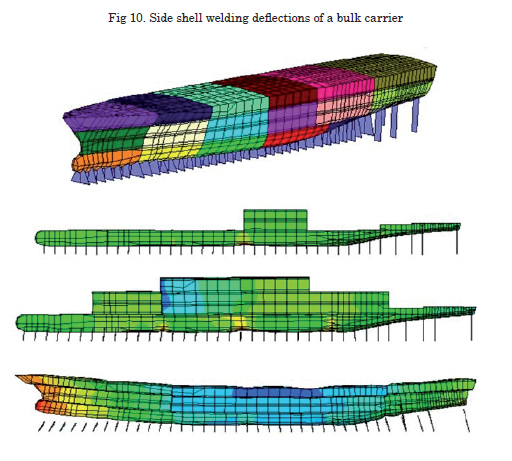
The second case represents the ship block assembly process. In this case, the welding distortion produced is predicted through the same elastic FEM proposed herein. The objective of this study was to obtain the best welding sequence to be used in assembling the blocks. This is because during block assembly, welding distortion appears in decks due to existing residual stress produced by previous welding.
Fig. 10 shows the results of welding distortion predicted by this method. As seen in the figure, it is possible to predict the welding distortion of a large structure like the ship block assembly process.
Conclusions
A method to predict welding distortion of complex welded structures on ships has been developed. In this method, the inherent strain of single welding pass is first predicted based on the given heating condition and plate thickness. Then, by using the inherent strain databases of influential factors, corrections necessary for the inherent strain are made. The same procedure is followed for each welding pass, according to the welding sequence. Through numerical analysis, it has been demonstrated that this method can be used to easily and accurately predict welding distortion of complex ship structures.
In addition, the computational time is much shorter than that used in the thermo-elastic-plastic FEM. In the present study, the total computational time of both the thermal analysis and the thermomechanical analysis is approximately 36 hours for the thermo-elastic-plastic FE model (Case 1); whereas, the computational time of the elastic FE model is shorter than one hour (including preprocessing). For more complex ship structures (Case 2), the computation time required for thermoelastic- plastic FEM proportionally increases with the number of welding passes, while that required in elastic FEM is approximately the same as in the first case.
Acknowledgement
Authors greatly appreciate the support of the National Secretary of Science and technology of Panama (SENACYT) through their program of grants for research and development. Also author would like to thanks to Isthmus Bureau of Shipping (CLASS IBS) for all their support in this research.
References
DENG, D. A.; MURAKAWA, H. AND LIANG, W. Comput. Methods Appl. Mech. Engrg. 196: 4613- 4627, 2007.
LIANG, W.; DENG, D. AND MURAKAWA, H. J. MATER. Process. Tech. 183: 219-255, 2007. Liang, W. et al., Transactions of JWRI. 33(1): 45-51, 2004.
LIU, C AND ZHANG, X. Sci. Technol. Weld. Join. 2009, 14 (1), 26-31. Murakawa, H. Mater. Sci. Forum. 539-543: 181-186, 2007.
MURAKAWA, H; LIANG, W. AND DENG, D. Transactions of JWRI. 34(1). 113-123, 2005.
NISHIKAWA, H. et al., H. Proc. Int. Soc. Offshore Polar Eng. Conf. Toulon, France. May 2004, ISOPE, 126-132.
SERIZAWA, H.; NISHIKAWA, H. AND MURAKAWA; H. Sci. technol. Weld. Join. 1282): 147-152, 2007. Wahab, M. et al., 2006, 85 (22), 35 - 43.