Integrating topology and shape optimization: a way to reduce weight in structural ship design

Germán A. Méndez Algarra,-a
Andrés Tovar Pérez, Ph.D.-b

Abstract

The Hybrid Cellular Automaton (HCA) algorithm is a methodology developed to simulate the process of functional adaptation in bones. The HCA algorithm combines elements of the cellular automaton (CA) paradigm with finite element analysis. This methodology has proved to be computationally efficient to solve topology optimization problems. In this paper, the HCA algorithm is integrated with a shape optimization algorithm that uses sequential quadratic programming. The geometry of the topologically optimized structure is converted into a two-dimensional solid model using an edge detection algorithm and parametric B-splines. An example problem of a Michell structure is presented. Also shown is the application of the shape optimization algorithm in the redesign of the lightening holes in the transverse floors of a riverine patrol vessel designed by COTECMAR. In both cases an appreciable weight reduction was obtained.

Key words: Computational structural design, Topology optimization, Shape optimization

Resumen

El método de los Autómatas Celulares Híbridos (HCA) para optimización topológica simula el proceso de adaptación funcional en estructuras óseas. El método HCA combina la técnica de los elementos finitos para análisis estructural con el paradigma de los Autómatas celulares (CA) para el diseño y ha demostrado ser una técnica efectiva para optimización topológica en estructuras continuas. En este trabajo se integra el método HCA con un algoritmo de optimización de forma que utiliza programación cuadrática secuencial. La geometría optimizada topológicamente es utilizada para construir un modelo bidimensional sólido aplicando un algoritmo de detección de bordes en imágenes y esplines paramétricos. Un ejemplo de una estructura Michell es presentado. También es presentada la aplicación de un algoritmo de optimización de forma en el diseño de unos aligeramientos en las varengas de un buque patrullero fluvial diseñado por COTECMAR. En ambos casos una apreciable reducción del peso fue obtenida.

Palabras claves: Diseño de estructuras, optimización topológica, optimización de forma

a Department of Mechanical and Mechatronic Engineering,
National University of Colombia
e-mail: gamendeza@unal.edu.co
b Department of Mechanical and Mechatronic Engineering,
National University of Colombia
e-mail: atovarp@unal.edu.co

Introduction

Optimization techniques applied to the structural design can provide the maximum benefit from the available resources. Adopting optimal design procedures converts the process of design into a sequence of rational decisions, while the indirect design is based in experience, creativity and random ideas of the design team. Two of the main fields of application for the structural optimization are the topology and the shape optimization techniques. Several works have been published, showing applications of these methods in different engineering fields [8, 13, 14, 18].

The goal of topology optimization is to find the optimal distribution of material in a finite volume. This maximizes a determined measure of mechanical performance under determined constraints [17]. The topology optimization algorithm selectively removes and relocates the material until optimal performance is reached [22]. However, this approach to structural optimization has some disadvantages. The resultant structure tends to present non-smooth edges, due to the design domain discretization [16]. Furthermore, it is common to find zones with relatively high stress in the resulting edges, with the potential to be improved [19].

In shape optimization the goal is to find the optimum profile for the structure components, while maximizing the performance under a given set of mechanical constraints [5]. This kind of optimization problems is very common in several fields of engineering; like electromagnetism, biomechanics, structural design and fluid-structure interaction applications [7, 11, 12]. There are different approaches to deal with a structural shape optimization problem. For the structural evaluation of the designs, the finite element and the boundary element methods are very popular. Nevertheless, there are proposals that intend to exceed the performance of these traditional methods [24]. The most employed approaches for the solution of the shape optimization problem are the basis vector and the shape perturbation methods [21].
This work intends to present a rational design methodology which integrates the Hybrid Cellular Automata method for topology optimization, (HCA) [20], with a shape optimization algorithm based on the shape perturbation approach, which applies the finite element method and uses Sequential Quadratic Programming (SQP) to solve the optimization problem.

To integrate effectively the topology and the shape optimization methods, an edge detection algorithm is used in conjuction with parametric B-splines modelling on the topologically optimized structure [3]. The resulting solid model is used as the initial design for the shape optimization algorithm.

Topology optimization using the Hybrid Cellular Automaton method

The Hybrid Cellular Automaton (HCA) method is intended to solve complex structural optimization problems in engineering. The premise of the HCA method is that complex static and dynamic problems can be decomposed into a set of simple local rules that operate over a large number of cellular automata (CAs) that only know local conditions [22]. The cellular automaton neighborhood has no size or location restraints, except for its being defined in the same way for all of the CAs. This is an idealization of a physical system in which space and time are discrete. Therefore, the computation of the local evolutionary rules can benefit from parallel computing capacity [20].

In the HCA method, the design variables for the algorithm correspond to the relative densities of each automata. The elastic modulus of an element is expressed as a function of the relative density as

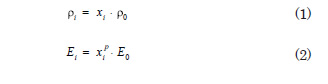
where and are the elastic modulus and density of the solid material, respectively, is a variable density. The power p is used as a penalization for intermediate relative densities, accordingly, helping to make the resultant design a black and white structure.

Along with the design variables, the state of each CA is determined by state variables . This variables are expressed as

where is the contribution of each element to the strain energy of the structure. The values of the state variables are determined using the Finite Element Method on each iteration of the algorithm.

The HCA algorithm solves a constrained optimization problem given by

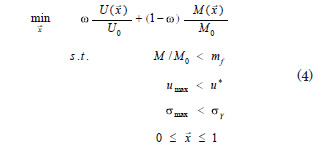
where is the total strain energy, is the mass of the structure and ω is a weight coefficient. The first constraint specifies the available mass to be used in the design. The second and third constraints impose limits on the resulting structural displacements and stresses. Finally, the design variables fluctuate between the boundaries 0 and 1. Actually, the lower limit is not 0 but a small positive value, to avoid the singularity in the stiffness matrix during the finite element analisys.

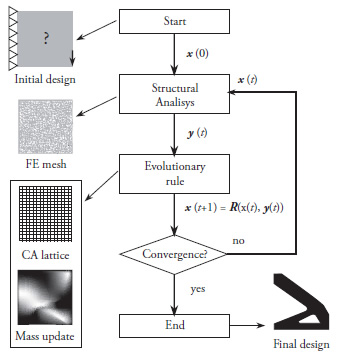
The HCA topology optimization algorithm, as shown in Fig. 1, can be described as follows. First, the design domain is defined, along with the physical properties of the material, load conditions and initial design. The analysis of stresses and displacements using the finite element method determines the values of the state variables. The value for the design variables is updated according to the local evolution rule . Then, the algorithm returns to the second step for the evaluation of the state variables. The convergence criterion is satisfied when there is no variation in the design variables, or when the maximum number of iterations is reached.

Shape optimization

Shape optimization for structural design aims to find the optimal profile or boundaries of a structure that minimizes certain objective function under specified mechanical constraints. The basis vector method and the shape perturbation method are the most common approaches to solve shape optimization problems [21].

In the basis vector approach, the shape of the structure is described by a combination of different trial designs called ‘basis vectors’. The design variables are the weighting parameters that define the participation of each basis vector in the design process.

On the other hand, the shape perturbation approach requires the definition of perturbation vectors. These vectors deform the boundary of the initial design domain. The design variables are constituted by the components of the perturbation vectors, which determine the amount of perturbation during the optimization process [9].
This work makes use of the grid perturbation approach. Therefore, since this work focuses on two dimensional domains, the design variables vector is composed by two perturbation values associated with each node in the model [1].

The shape optimization problem with nonlinear constraints can be expressed as

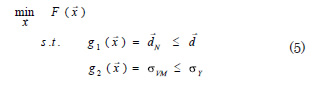
where is the design variables vector, is the vector with the magnitude of the displacement for each node, and is the maximum value of von Mises stress in the model. To solve this optimization problem the sequential quadratic programming (SQP) approach is employed.

Design variables

The horizontal and vertical coordinates that define the location of the ith node of the model, and respectively, are defined by

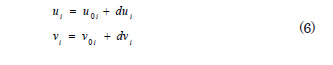
where and are the coordinates of the ith node on the initial design, and and are, respectively, the horizontal and vertical perturbation on the same node. The design variables vector can be written as

where , for i=1,2,…, n; with n being equal to the number of non-restrained nodes in the model. It follows that during the construction of the design variables vector it is necessary to define an adequate objective for the final shape.

Objective function

In order to obtain the desired complement between the topology optimization and the shape optimization algorithms, it is necessary an adequate definition of the objective for the last one. The shape optimization method developed for this work uses the weight of the structure as objective function. In the two-dimensional domain this function can be expressed as

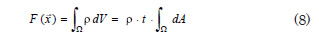
where t is the thickness of the element and ρ is the material’s density.

The objective function requires the calculation of the area contained by each contour, then, the values for the interior loops are subtracted from the exterior contour. Thus, the objective function takes the form of

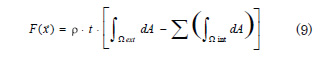
Displacement constraint

The displacement constraint is imposed in order to maintain the geometric validity of the model. This constraint can be expressed as

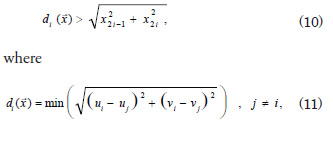
and and are, respectively, the horizontal and vertical coordinates of the node. The application of this constraint can significantly affect the performance of the optimization algorithm if a high number of nodes are used to describe the design boundaries.

Stress constraint

In order to maintain the required consistency between the topology and the shape optimization method, a stress constraint is imposed. This guarantees that the design is stiff enough to endure the load. The failure criterion used in this case is von Mises, due to its conservative results and simplicity of implementation. The von Mises criterion for ductile materials undergoing a general state of stress is defined as

This can be seen as the volume contained in a cylinder with radius with a symmetry axe forming equal angles with the principal stress axes. This expression, for materials under plane stress, is reduced to

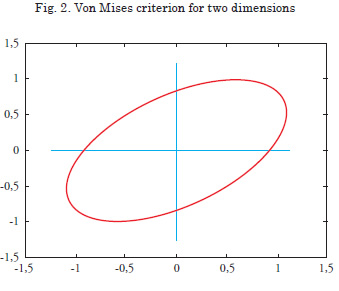
which represents the area of a rotated ellipse Fig. 2. The evaluation of this constraint requires a finite element analysis of the plane stress model on each iteration. The maximum Von Mises stress found in the model is compared with the permissible stress established for the problem. The allowable stress can be the yield stress for the material or can include a design safety factor.

Integration of topology and shape optimization

In order to achieve the integration of the topology (TO) and shape optimization (SO) algorithms, it is necessary to apply an intermediate processing. The idea is to convert the result of the TO into a valid model usable as the initial design for the SO [23].

The result of the execution of the topology optimization algorithm is a matrix with the values of the relative densities of the cellular automata. A grayscale image that describes the shape of the structure can be obtained by using the design variables results as intensity values. Ideally a black-and-white image will be obtained; however, it is common to obtain some automata with intermediate relative density values.

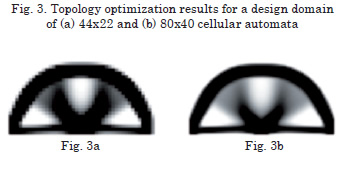
In this image, one pixel corresponds to one cellular automaton. In consequence, the resolution of the image depends on the number of automata selected for the topology optimization algorithm. Therefore, the smoothness of the contours varies according to the discretization of the design domain, as shown in Fig. 3.

An edge detection algorithm is applied to the image obtained using the topology optimization. The Canny method for edge detection, considered the optimal method for edge detection on digital images [6], is used.

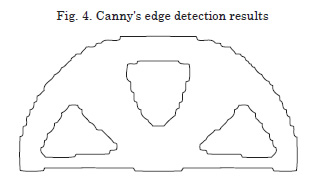
The edge detection process reduces the information contained in the image, preserving the main structural properties [10]. The application of the Canny method to the image shown in Fig. 3a results in the image of the edges as seen in the Fig. 4.

The next step to obtain the initial design for the shape optimization algorithm is to create a b-spline model for each contour in the image. By means of this, the contours of the model are smoothed [3].

At this point, the density of control points for the b-spline modeling is established . This parameter for the node density, , sets the percentage of points on the edge image preserved as a node for the b-splines, and is expressed as

where is the number of nodes in the b-spline model and is the quantity of black pixels in the image obtained with the edge detector.

Since every node has two perturbation values associated as design variables in the grid perturbation method used in the shape optimization algorithm, this parameter directly determines the number of design variables for the shape optimization problem. Moreover, the density of control points is important in the definition of the displacement constraints and, consequently, an inadequate value can affect the performance of the algorithm.

Once the contours are modeled as b-splines, a solid model is generated by the subtraction of the interior portions from the exterior part. At this point the geometric model of the initial design is complete. The remaining step is to translate the boundary conditions of the problem (loads and restraints) to the corresponding nodes in this geometric model.

Application example

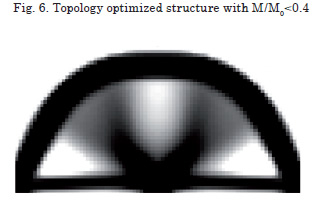
To illustrate the performance of the integrated methodology, the design of a two-dimensional Michell-type structure is considered [15]. The design domain has an area of 800 ∙ 400 mm2 with a thickness of 20 mm. The displacement of the left lower corner is restrained in both directions and the displacement of the opposite lower corner is constrained in the vertical direction. The design domain is discretized into 80 ∙ 40 identical cellular automata. The properties of A-36 steel are used, and a vertical load of 5000 N is applied in the middle of the lower border, Fig. 5.

Defining the mass constraint limit to , the HCA algorithm converges in 24 iterations to the result displayed in the Fig. 6.

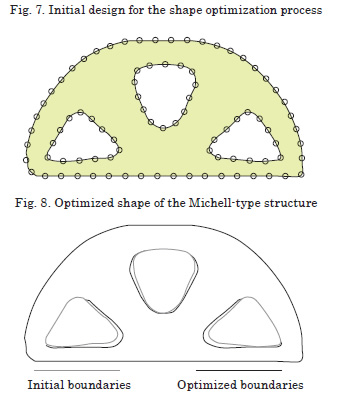
The application of the method to construct the shape optimization initial design, given the node density parameter a value of K=0.04, produces the model shown in Fig. 7. After the shape optimization process, a 4.47% reduction in weight is achieved. The algorithm converged, after 13 iterations, to the shapes presented in Fig. 8.

Shape optimization of structural floors in the PAFL

As an application of the shape optimization algorithm developed for this work, the reshape of the transverse floors in the parallel body of the riverine patrol vessel (PAFL for its Spanish acronym), designed by COTECMAR, the Science and Technology Corporation for the Naval, Maritime and Riverine Industries, is considered (see Fig. 9).

Initially, these elements were designed following the ABS Rules for building steel vessels for service on rivers [2]. As the operational profile of the ship requires a very low draft, the structural weight minimization is a primary objective for the next unit. The use of a documented direct calculus method, like the shape optimization presented here, enables the design to exceed the limits of the Classification Society rules.

The initial design for the shape optimization problem is extracted from the arrangement obtained applying the ABS Rules. The load condition includes the buoyancy pressure on the hull and, on the upper edge, the pressure from the maximum liquid column in case of damage to the compartment immediately above, as shown in the Fig. 10. The material used for the element is naval steel ASTM A131 [4].

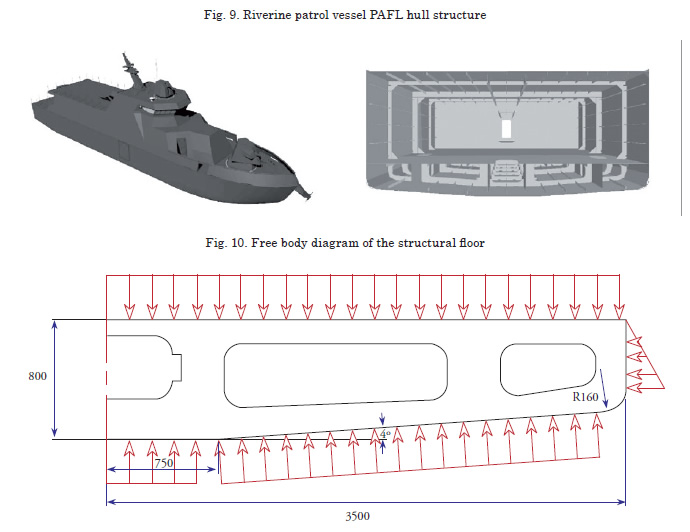
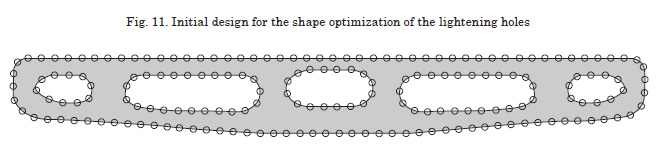
Fig. 11 shows the b-spline model of the initial design. Since the hull and inner bottom forms cannot be altered, the perturbation of the shape is only possible in the interior boundaries. The load condition is introduced as nodal loads in the bottom and tank top edges. The displacements for the extreme nodes in the inner bottom are restrained.

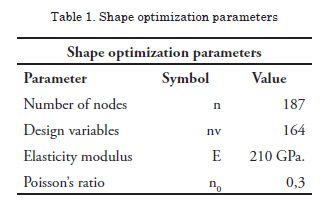
Table 1 shows the shape optimization problem parameters used for the reshape of the transverse floors.

The convergence criterion for this problem is satisfied when no change occurs in the objective function, which means that

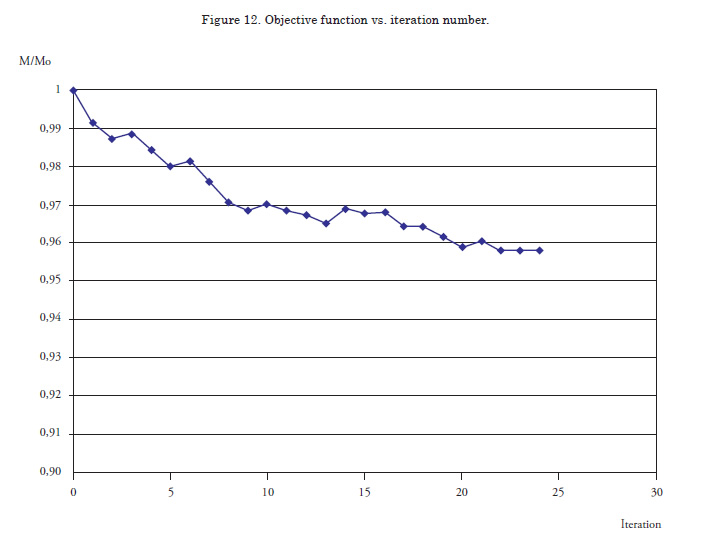
After 24 iterations, convergence is obtained to an objective function value of 15947, equivalent to a 4.21 % reduction in weight of the structure. The objective function values and the final shape are shown in the Fig. 12.

Conclusions

This first attempt for the integration of the Hybrid Cellular Automata method with a shape optimization algorithm constitutes a tool for structural design with applications in several fields of engineering. The design tool is particularly useful in applications where the reduction of weight is an upmost objective. The addition of the shape optimization algorithm, in conjunction with the edge smoothing, improves the weight reduction.

The use of this methodology in early stages of the design process of river vessels, where reduced draft is of primary importance, enables an appreciable reduction in the weight in some of the main structural components. Current work focuses in the refinement of the shape optimization algorithm and the exploration of other types of approaches, like evolutionary methods.
For each design case, the node density in the construction of the initial design for the shape optimization method must be selected with caution. The compromise between the desired level of detail and the computational cost must be considered and the sensibility of the results to the variation of this parameter is a subject of current analysis.

Further work will include the extension of the topology optimization to the design of plate structural members of ships, like the transverse floor shown in the example. This will include the constraints in the design domain that take account of the hull shape.

Acknowledgements

The authors would like to thank the Science and Technology Corporation for the Naval, Maritime and Riverine Industries, COTECMAR, for the support and assistance in this project. We also thank the anonymous referee for the detailed review of our paper and the important comments provided.

References

[1] ALLAIRE, G. Shape Optimization By the Homogenization Method. Springer, 2001.

[2] AMERICAN BUREAU OF SHIPPING,. Rules for building and classing. Steel vessels for service on rivers and intracoastal waterways. ABS, 2007.

[3] ANNICCHIARICO, W., AND CERROLAZA, M. Finite elements, genetic algorithms and beta-splines: a combined technique for shape optimization. Finite Elements in Analysis and Design 33 (1999), 125–141.

[4] ASTM STANDARD A 131/A 131M 2004,. Standard Specification for Structural Steel for Ships. ASTM, DOI: 10.1520/A0131_A0131M-04, www.astm.org, 2004.

[5] BENDSOE, M. P. Optimal shape design as a material distribution problem. Structural and Multidisciplinary Optimization 1 (1989), 193–202.

[6] CANNY, J. A computational approach to edge detection. PAMI 8 (1986), 679–698.

[7] CEA, J., GARREAU, S., GUILLAURME, P., AND MASMOUDI, M. The shape and topological optimizations connection. Computer Methods in Applied Mechanics and Engineering 188 (2000), 713–726.

[8] CHIANDUSSI, G., GAVIGLIO, I., AND IBBA, A. Topology optimization of an automotive component without final volume constraint specification. Advances in Engineering Software 35 (2004), 609–617.

[9] GIVOLI, D., AND DEMCHENKO, T. A boundary-perturbation finite element approach for shape optimization. International Journal for Numerical Methods in Engineering 47 (2000), 801–819.

[10] GONZALEZ, R., AND WOODS, R. Digital Image Processing. Prentice Hall, 2002.

[11] HÄUßLER, P. Topology and shape optimization methods for cfd problems. In CADFEM Users’ Meeting, Fellbach (2006).

[12] KEGL, M., AND BRANK, B. Shape optimization of truss-stiffened shell structures with variable thickness. Computer Methods in Applied Mechanics and Engineering 195 (2006), 2611–2634.

[13] MACHADO, G., AND TRABUCHO, L. Some results in topology optimization applied biomechanics. Computers & Structures 82 (2004), 1389–1397.

[14] MACKERLE, J. Topology and shape optimization of structures using fem and bem. a bibliography (1999 - 2001). Finite Elements in Analysis and Design 39 (2003), 243–253.

[15] MICHELL, A. The limits of economy of material in frame-structures. Philosophical Magazine 8 (1904), 589–597.

[16] PEREIRA, J., FANCELLO, E., AND BARCELLOS, C. Topology optimization of continuum structures with material failure constraints. Structural and Multidisciplinary Optimization 26 (2004), 50–66.

[17] ROZVANY, G. Aims, scope, methods, history and unified terminology of computer aided topology optimization in structural mechanics. Structural and Multidisciplinary Optimization 21 (2001), 90–108.

[18] SIGMUND, O., AND TORQUATO, S. Design of materials with extreme thermal expansion using a three-phase topology optimization method. Journal of the Mechanics and Physics of Solids 45 (1997), 1037–1067.

[19] TANG, P., AND CHANG, K. Integration of topology and shape optimization for design of structural components. Structural and Multidisciplinary Optimization 22 (2001), 65–82.

[20] TOVAR, A. Optimización topológica con la técnica de los autómatas celulares híbridos. Rev Int Mét Num Cálc Dis Ing 21 (2005), 365–383.

[21] TOVAR, A., GANO, S., MASON, J., AND RENAUD, J. Optimum design of an interbody implant for lumbar spine fixation. Advances in Engineering Software 36 (2005), 634–642.

[22] TOVAR, A., PATEL, N., NIEBUR, G., SEN, M., AND RENAUD, J. Topology optimization using a hybrid cellular automaton method with local control rules. Journal of Mechanical Design 128 (2006), 1205–1216.

[23] YILDIZ, A., ÖZTÜRK, N., KAYA, N., AND ÖZTÜRK, F. Integrated optimal topology design and shape optimization using neural networks. Structural and Multidisciplinary Optimization 25 (2003), 251–260.

[24] ZHANG, X., RAYASAM, M., AND SUBBARAYAN, G. A meshless, compositional approach to shape optimal design. Computer Methods in Applied Mechanics and Engineering 196 (2007), 2130–2146.