Applications of optimization in early stage ship design

Recent research at the University of Michigan developing and applying modern optimization methods to early ship design decision making is reviewed. These examples illustrate the use of fuzzy logic, genetic and evolutionary algorithms, and agent methods to solve complex multicriterion ship design problems. The first application optimizes an early stage hull form for both smooth water powering and seakeeping performance using an advanced evolutionary algorithm taking into consideration the change of vessel weight with the hull form variation. The second application supports the optimization of naval ship general arrangements using a new hybrid agent-genetic algorithm method and stochastic generation algorithm. The final example uses an evolutionary algorithm to establish the optimal commonality to use in two ship classes that are to share components and features in order to save overall fleet costs. These show how these advanced ship design methods can be used to aid early ship design decisions.

Key words: Ship design, multicriterion optimization, genetic algorithms, evolutionary algorithms, agent methods, fuzzy optimization

Se presenta una revisión de recientes investigaciones realizadas en la Universidad de Michigan que desarrollan y aplican métodos modernos de optimización en la toma de decisiones en las primeras etapas del diseño de embarcaciones. Problemas complejos de optimización multicriterio en el diseño de buques son resueltos utilizando lógica difusa, algoritmos evolutivos y métodos de agentes. En la primera aplicación se optimiza la forma del casco en una etapa preliminar para optimizar tanto la potencia requerida en aguas tranquilas como el comportamiento en el mar usando un algoritmo evolutivo que considera el cambio en el peso del buque ocasionado por la variación en la forma del casco. La segunda aplicación utiliza un método híbrido agentes-genético y generación estocástica para soportar la optimización del arreglo general de unidades navales. Por último se utiliza un algoritmo evolutivo para optimizar la concordancia de componentes usados en dos clases de buques con el fin de reducir el costo global de la flota. Estos ejemplos muestran la ayuda que proporciona la utilización de métodos avanzados de diseño en la toma de decisiones durante las primeras etapas del diseño de buques.

Key words: Ship design, multicriterion optimization, genetic algorithms, evolutionary algorithms, agent methods, fuzzy optimization.

^aArthur F. Thurnau. Professor Emeritus Department of Naval Architecture and Marine Engineering,
e-mail: parsons@umich.edu

............................................................................................................................................................

Ship design involves the careful balancing and optimization of many complex, interacting issues. Formal numerical optimization methods were long unable to deliver on their promise, however, because of their limited capability to handle problems complex enough to really address the important design issues in naval ship design. This situation has changed in recent years with the evolution of computer power, the development of increasingly complex analysis and synthesis capabilities, and the development of new methods to treat complex, multicriterion optimization problems. Many of these methods evolved in the broad area of artificial intelligence and soft computing over the past three decades. The author has worked in this area for more than 20 years and taught this material in the graduate-level design class NA570 Advanced Marine Design at the University of Michigan from its introduction in 1997 until his retirement from the University in May 2008. Three areas of research using these methods are described here to illustrate some the capabilities and potential of these methods to address important ship design issues.

Most ship design problems involve multiple conflicting criteria for selecting the best design, such as the inevitable tradeoff between performance and cost. Marine design requires the careful consideration of these competing criteria and experienced marine designers must make difficult design tradeoff decisions. Traditional numerical optimization methods were first developed for use with a single optimization criterion, objective function, measures of merit, or cost function. These early numerical optimization methods had some success in detailed design decisions, but they were significantly less effective in solving higher-level conceptual and preliminary design problems involving multiple conflicting criteria. And this is precisely the area were the greatest gains can be achieved by formal optimization.

The multicriterion optimization problem involves K ≥ 1 criteria and can be formulated in the form:

where the K multiple optimization criteria

through

are each dependent upon the N unknown design parameters in the vector x. In general, this problem has no single solution due to the conflicts that typically exist among the K optimization criteria.

The traditional approach to solving this type of problem with early numerical methods that could handle only one criterion was to use a weighted-sum cost function to convert the vector F into a related scalar cost function F. There are also a number of scalar compromise solution definitions, such as the min-max and nearest to the utopian solutions, which can be used if a particular definition reasonably reflects a design team’s intent. These methods were reviewed and compared in Parsons and Scott (2004).
When conflicting multiple criteria are present, the most common definition of an optimum is Pareto optimality, which was first articulated by the Italian-French economist V. Pareto (Pareto 1906). This is also referred to today as Edgeworth-Pareto optimality (Statnikov 1999) and can be expressed as, A design is Pareto optimal if it satisfies the constraints and is such that no criterion can be further improved without causing at least one of the other criteria to decline.

Note that this recognizes the conflicting or competitive interaction among the criteria. If there are conflicting criteria, Pareto optimality results in a set of solutions that are all considered equally good under this definition. Some additional consideration must be used to select the resulting single design to use. Compromise solutions, e.g. the min-max solution noted above, might be used to help in the selection of one particular design solution to use. The Pareto set or Pareto front that results from the minimization of two criteria

and

is illustrated schematically in Fig. 1. This shows the two criteria normalized by the best or minimum value achieved for that criterion. The Pareto front extends between the solution that yields the best for criterion one,

, to the solution that yields the best for criterion 2,

. It may contain gaps if the feasible region is not convex. The min-max compromise solution is one on the 45o line in this normalized presentation. Designers often focus on the “knees” of the front where there is a sharp change of slope. These solutions are considered more efficient since the loss of one criterion begins to increase more rapidly with each improvement in the other.

Most recent applications of multicriterion design optimization have utilized genetic algorithms (GA's) to find the scalar solution or generate the Pareto front. GA’s have evolved out of John Holland's pioneering work (Holland, 1975) and Goldberg’s engineering dissertation at the University of Michigan (Goldberg, 1983). These optimization algorithms typically include operations modeled after the natural biological processes of natural selection or survival, reproduction, and mutation. They are probabilistic and have the major advantage that they can have a very high probability of locating the global optimum and not just one of the local optima if they are present in a particular problem.

GA’s can readily treat a mixture of integer, discrete, and real variables in x. The unknown vector x is typically coded as a binary string called a chromosome. These algorithms are also called evolutionary algorithms when the unknowns are coded as real rather than binary variables. GA's operate on a population of potential solutions at each iteration or generation rather than evolve a single solution, as do most conventional optimization methods. Constraints can be handled through a penalty function or applied directly within the genetic operations. These genetic algorithms require significant computation, but this is much less important today with the dramatic advances in computing power. Accessible general references on GA’s are by Goldberg (1989), Coley (1999), and Gen and Chang (2000). Independent variable coding is well treated by Michalewicz (1996).

In GA’s, an initial population of solutions or individuals (chromosomes) is randomly generated in accordance with the underlying constraints and then each individual is evaluated for its fitness for survival. The definition of the fitness function is for maximization, but can achieve either minimization or maximization through the formulation. The genetic operators work on the chromosomes within a generation to create the next, usually improved generation with a higher average fitness. Individuals with higher fitness for survival in one generation are more likely to survive and breed with each other to produce offspring with even better characteristics, whereas less fit individuals will eventually die out. After a large number of generations, a globally optimal (or near-optimal) solution or the Pareto front can generally be reached.

Three genetic operators are utilized in a simplest genetic algorithm. These are selection, crossover, and mutation operators (Goldberg, 1989, Li and Parsons, 2001). The selection operator selects individuals from one generation to form the core of the next generation according to a set random selection scheme. Although random, the selection is biased toward better-fitted individuals so that they are more likely to be copied into the next generation. The crossover operator combines two randomly selected parent chromosomes to create two new offspring by interchanging or combining gene segments from the parents. The mutation operator provides a means to alter a randomly selected gene(s) of a randomly selected single chromosome to introduce new variability into the population. Crossover and mutation provide the random search capability to locate the region of the global solution. Many algorithms include an elitism mechanism to ensure that the current best solution(s) is not lost through the genetic manipulations.

GA’s and evolutionary algorithms have been adapted to multicriterion optimization where they are particularly attractive because they can generate the whole Pareto front in one optimization run. The algorithms are especially adapted to generate a population of solutions along the Pareto front by dominance sorting of the population at each generation to retain those that satisfy the Pareto optimum definition. Evolutionary algorithms for solving multicriterion optimization are well treated by Deb (2001), Osyczka (2002), and Zitzler et al. (2003).

Many important engineering design problems involve issues that are subjective, vague, or ambiguous. Fuzzy set theory provides a way to deal with these issues. Fuzzy set theory, started by Zadeh (1965), introduced the concept that rather than requiring that something had to be a member of a set (1) or not (0), the traditional crisp sets, it could have a varying degree of membership μ(x) between zero and one. This allows subjective, vague and ambiguous things to be modeled rigorously for treatment in control systems, optimization, etc. By using fuzzy sets computations can be performed in linguistic terms (using set names) that mimic complex human reasoning. Good introductions to fuzzy sets and systems are provided in Zimmerman (1991), Kosko (1992), and Mendel (2001). Li and Parsons (1998) used fuzzy decision models to model the aggregate behavior of the world shipping community in buying, selling secondhand, and scrapping tankers (1998).

A helpful example is the concept of a person being tall. This is a subjective thing that depends upon the context – is it a basketball or horse racing jockey locker room? In traditional (crisp) set theory, a person would have to be either a “tall person” or a “not tall person.” A person of normal height under normal situations might make this transition at 5’10” (1.78 m). The crisp set membership functions or truth value μ(height) for this are shown as the solid lines in Fig. 2. The membership must be either zero or one. Using fuzzy sets, one could more realistically say that a person is definitely a “not tall person” if they are 5’6” (1.68 m) or less and that they are definitely a “tall person” if they are 6’2” (1.88 m) or taller. Between these two heights there is a gradual, fuzzy transition from being not tall to being tall. The fuzzy set membership functions μ for this are shown as the dashed lines in Fig. 2.

In fuzzy optimization, fuzzy membership functions or fuzzy utilities 0 ≤ U(x) ≤ 1 are defined for each criterion or constraint. They represent the degree to which some requirement is satisfied. The independent variable x is selected to appropriately reflect each issue. A typical fuzzy utility, as might be used to express a requirement for ship speed to accomplish a particular mission, is shown in Fig. 3. The region with U(x) = 0 is clearly unacceptable to the designer and region with U(x) = 1 is fully acceptable. The fuzzy region between the minimum acceptable threshold x and the design goal or target

is a subjective, fuzzy quantity between 0 and 1. This is similar to the approach used by Brown and Salcedo (2003) to define naval design Measures of Performance (MOPs) for their use in performance and cost multicriterion optimization for a DDG. The fuzzy transition could be developed by design judgment or from expert opinion by using the Analytical Hierarchy Process (Saaty, 1996).

If each design goal and constraint is expressed by an appropriate utility function

that depends on the design choices x, a fuzzy optimum using minimum correlation inference (Kosko, 1992), for example, is given by the maximization of the optimization criterion (cost function) or total utility

This seeks the design x that maximizes the worst (minimum) satisfaction of any of the applicable goals and constraints i. This approach yields a multicriterion compromise among all of the conflicting goals and constraints and treats them all in a similar manner. It has the search advantage that there can always be a “feasible” solution that can be improved.

The naval combatant hull form that minimizes smooth water powering will generally not provide the best seakeeping performance. This design tradeoff was a major focus of the U.S. Navy DDG51 design process (Keane and Sandberg, 1984). The goal of the first research to be reviewed here (Zalek et al., 2006a; Zalek et al., 2006b; Zalek, 2007; Zalek et al., 2009) was to develop a multicriterion design optimization scheme that would take the ship design description and hull offsets produced by the U.S. Navy’s Advanced Surface Ship Evaluation Tool synthesis model (ASSET, 2005) and optimize the hull form for smooth water powering and seakeeping performance. To maintain the validity of the parent ship analysis performed by ASSET, the search for the hull form parameters and variables was allowed to vary roughly ±15% from the parent design. This limitation was imposed to provide assurance that the final hull would still meet the mission effectiveness provided by ASSET, which considers much more detail about the overall design.

The example shown here will be the optimization of a frigate parent produced by ASSET. The parent hull parameters and the range of variation of the parameters permitted in the optimization are shown in Table 1. The depth D is fixed by the accumulation of deck heights and the blade number

is fixed by typical practice.

The performance criteria were the minimization of required power for smooth water operations and the minimization of the probability of the vessel’s failure to complete its missions due to overall seakeeping performance. The power minimization criterion was as follows:

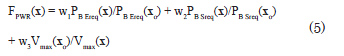
where the weights

sum to one. This combines the brake power required for the endurance speed

, the brake power required for sustained sea speed

, and the maximum vessel speed

. Each is normalized by its value for the parent hull,

. The inversion of the final term changes maxVmax to the equivalent

The seakeeping criterion was expressed as an inoperability index to be minimized,

where

, between 0 and 1, is the U.S. Navy’s seakeeping operability index as presented by Keane and Sandberg (1984):

This operability index calculates the Expected Value (probability) of the vessel being able to complete its missions m as determined by the associated seakeeping limits

at locations (X, Y, Z) on the ship for the various headings

, speeds

, Sea States

that will be encountered. The summation Σ is a discrete integration overall all missions m, headings j, speeds k, and Sea States ℓ. The function f is either 0 or 1 for each jkℓm depending upon whether on not the ship can satisfy all the limits

in mission m at their associated location (X, Y, Z) in the seakeeping analysis for condition jkℓ. P is the probability of occurrence of the given heading, speed, Sea State, and mission in jkℓm.

For the example below, the speed profile

was adapted from data for DDG51 as shown in Table 2. The probability of occurrence of the Sea States

were for year-round conditions in the North Atlantic as shown in Table 3. The three missions (activities) m and their associated seakeeping limits and locations were as shown in Table 4. All heading angles relative to the waves

were considered equally likely.

The power required was calculated using an adaptation of the model of Holtrop and Mennen (1982) and Holtrop (1984) using the wetted surface calculated from the vessel offsets. The propeller design was optimized in an inner loop calculation using an adaptation of the Wageningen B-Screw Series Propeller Optimization Program (POP) presented in Parsons et al. (1998). The seakeeping performance was calculated using an adaptation of the linear, frequency-domain, slender-body strip theory code SHIPMO.BM developed by Beck and Troesch (1989). Viscous roll damping based upon Himeno (1981) is added within SHIPMO.BM.

The ship design modeling included constraints to keep the independent variables within a reasonable distance of the parent hull initial values

as shown in Table 1 to ensure that the more complete analyses of ASSET would still be reasonably valid for the resulting optimized hull design. In practice, ASSET would also be rerun for the optimized hull design to ensure that the overall design was viable. One unique aspect of this work was the use of the full 346 three-digit weight group models from ASSET within the optimization so that the vessel would always have realistic weight estimates as the hull form changes and satisfies weight-equals-displacement. Prior hull form optimization has typically assumed constant displacement so that this major complexity could be avoided. Zalek shows that this is a poor assumption that will yield results far from the Pareto front (Zalek, 2007). The weight was made equal to displacement within 0.05% by establishing either draft T or midship coefficient

internally as a dependent variable.

The longitudinal center of gravity LCG and longitudinal center of buoyancy LCB were assumed to have enough later design flexibility to provide the desired even keel trim.

Inequality constraints, some mandatory and others optional, were included to ensure the minimum required GMT, minimum required deck area, minimum required machinery space length and depth, minimum deck height, propeller characteristic and cavitation limits, maximum required sustained speed power, and maximum required throttle setting.

The hull form changes required to yield the design parameters were made systematically to ensure that the resulting hull was always a fair and reasonable hull. The method developed by Zalek modifies the offsets in four phases to (1) match the length on the waterline, beam, and draft; (2) match the hull prismatic coefficient and longitudinal center of buoyancy; (3) match the waterplane coefficient and longitudinal center of flotation; and then (4) modify each station’s offsets to match the area and constraints derived from the first three phases (Zalek et al., 2008).

Zalek (2007) used a nontraditional multicriterion formulation that contains five criteria,

where D(x) is a diversity operator that attempts for force the solutions to spread out along the Pareto front for good definition, H(x) is a penalty term to force weight to equal displacement, and G(x) is a penalty term to force satisfaction of the inequality constraints (Zalek, 2007; Zalek et al., 2009). The diversity operator forces each group of three nearest neighbor solutions along the Pareto front to be as far apart as possible.

The solution was obtained using a multicriterion evolutionary algorithm developed by Zalek (Zalek, 2007; Zalek et al., 2009). At each generation, the initial population of solutions and those developed by the genetic operators were subject to a non-dominance sorting in accordance with the Pareto optimality definition. The initial population was generated at random. The highest ranked solutions were placed in an archive that serves as the elitism mechanism. These were then subjected to tournament selection to produce parents for arithmetic crossover. These offspring were then added to the archive with others produced by mutation and the process was repeated to select the new non-dominated solutions that approximate the Pareto front.

Figure 4 shows the results from a typical optimization run starting with the triangle solutions in the first generation and proceeding to the diamond solutions after 120 generations, which provide a good numerical approximation to the Pareto front. The results are shown in the primary criterion space

. The solution at the upper left provides the lowest power requirement and the solution at the lower right provides the best seakeeping performance.

The resulting Pareto Front designs for the optimized ASSET produced frigate hull form are shown in the normalized optimization criterion space in Figure 5. The power weights

were (0.4, 0.4, 0.2), the endurance speed was 20 knots, and the sustained speed was 28 knots. The best powering design and the best seakeeping design are shown. The min-max compromise design is also shown. In this case, this also happens to be the nearest design to the utopian point

, which cannot be achieved due to the inequality constraints. Note that the diversity operator has produced a good definition to the entire Pareto front by ensuring that all non-dominated designs are spread out along the front.

The characteristics of the parent design produced by ASSET and the best smooth water powering, best seakeeping, and min-max compromise optimized designs are shown in Table 5. The best powering design is relatively short, narrow, and deep in the water. The best seakeeping design is almost 23 m longer, wider, and almost 1 m shallower. Both designs use the same GE LM2500-21 engine. As expected the min-max compromise design is intermediate between these two designs. Note that it achieves excellent

powering and FSK seakeeping performance, each within about 3.4% of the best possible. The body plans of the resulting hull forms for these designs are shown in Zalek et al. (2009).

The creation of effective general arrangements in naval vessels is a difficult design task requiring considerable time and the consideration of many potentially conflicting design goals, requirements, and constraints. The overall goal of the second research to be reviewed here (Daniels and Parsons, 2006; Nick et al., 2006; Nick and Parsons, 2007; Daniels and Parsons, 2007; Nick, 2008; Daniels and Parsons, 2008; Parsons et al., 2009) was to provide an optimization technology and design tool to assist the arrangements designer to create effective naval surface ship arrangements with the maximum amount of intelligent decision making support. The software system will assist the designer in developing rationally-based arrangements that satisfy design specific needs as well as general Navy requirements and standard practices to the maximum extent practicable. This system will be used following or as a latter part of U.S. Navy’s ASSET (2005) synthesis process. It is compatible with the U.S. Navy’s product modeling and database system LEAPS (2006).

The arrangement process is approached as two essentially two-dimensional tasks as shown schematically in Fig. 6. First, the spaces are allocated to Zone-decks, one deck in one vertical zone, on the ship’s inboard profile using fuzzy optimization. Then the assigned spaces are arranged in detail on the deck plan of each Zone-deck in succession. The arrangement phase is divided into two coupled parts: the fuzzy optimization of the topology (relative location) of the spaces within the Zone-deck where each topology uses the best of multiple detailed geometries generated by a stochastic generation algorithm. Consideration is given to the desired overall location, adjacency, separation, access, area requirements, area utilization, and effective compartment shape. The modeling can produce rectangular, C, T, L, and Z-shaped spaces as needed to fit around each other, stair towers, vent trunks, weapons modules, etc.

The allocation modeling used a real integer independent variable vector, chromosome, that indicates the Zone-deck k to which each space i is allocated,

This ensures that each space is assigned to one and only one Zone-deck without additional constraints. The search space is very large. A corvette-sized vessel with I = 89 assignable spaces and K = 29 Zone-decks will have a theoretical search space (possible x solutions) of

. At this strategic design stage, the efficient utilization of available arrangeable space in the Zone-decks and the desired global location, adjacency and separation of the spaces are considered. The fuzzy optimization criterion used was follows:

The first term uses minimum correlation inference and seeks to raise the worst of the area utilization fuzzy utilities for the Zone-decks as shown in Fig. 7 where the design seeks a utilization UUk = allocated area/available area of 95% of the available area. This model uses the formula for the Normal distribution for the each half of the continuous utility and the designer can control σℓ and σu. The second term seeks to raise the average area utilization utility for all Zone-decks. The third term seeks to raise the weighted average of the least satisfied of the Ni global location goals and adjacency and separation constraints for each space i. Weights are used so that a Combat Information Center (CIC), for example, can have greater priority than a storeroom. Since this optimization involves assignment to discrete Zone-decks, the UiNi fuzzy utilities are discrete values, between 0 and 1, that depend upon the current Zone-deck of space i and the Zone-deck of the space j to which adjacency and separation constraints are given.

The geometry modeling involves the use of the three-box model in which each space has a centroid rectangle and can then grow up to two appendage rectangles to create L, T, C, or Z shapes as needed. The initial development was on a 1 m x 1 m grid system. An example topology chromosome for a Damage Control Deck Zone-deck to which spaces 1 through 14 have been allocated could appear as follows:

where PP and SP indicate the prearranged location of the main fore and aft port and starboard passageways, respectively, and CP indicates the location of an arrangeable cross passage. This topology indicates that spaces 1, 3, 2 are arranged from fore to aft in the area outboard of the port passageway to which they were allocated. The best geometry generated by the stochastic growth algorithm for this topology chromosome is shown in Fig. 8 where the ST indicate stair towers and there is a fixed object trunk on the port side. Space 7 can be seen to use all three of its possible rectangles in order to fit around the stair tower and space 10.

where the

are the

constraint utilities for space i. The fuzzy utilities

are for the required area, minimum overall dimension, minimum segment width, aspect ratio, perimeter, adjacencies and separations, and if two accesses are required to the space, the access separation. One or two accesses can be specified to either main passage or left free.

The stochastic growth algorithm (Nick, 2008) starts with the space “centroid” locations indicated by the chromosome and then generates the spaces by a random process of expanding and shrinking the spaces until the total space is filled. The space, direction of change, and amount of growth (±) are determined randomly with controlled probabilities. Moves are accepted if there is room for the change. Spaces can push a stair tower if there is room. Above and below the Damage Control Deck, the stair towers become fixed objects. Multiple geometries are generated for each topology chromosome and then the one giving the best utility, equation (12), is used in the optimization.

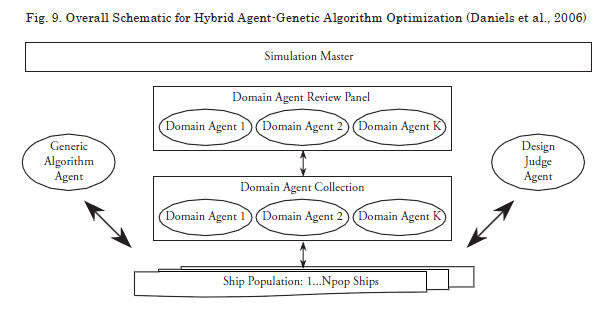
Daniels (Daniels and Parsons, 2008) developed a new hybrid agent-Genetic Algorithm optimization method for the allocation optimization. Agents are computer objects that are given a predefined behavior and are then allowed to operate to evolve a solution to complex problems. The allocation criterion, equation (10) has portions related to good design from the viewpoint of each Zone-decks,

, and portions related to good design from the viewpoint of each space, min

. This is amenable to an agent approach if there is an agent representing the in interests of each Zone-deck k and an agent representing the interests of each space i. The overall schematic is shown in Fig. 9.

The agent approach uses K Zone-deck Design Agents that sequentially propose a prioritized list of changes to a randomly selected candidate design that will improve its own area utilization utility

. The Zone-deck agents can propose to add a space, divest itself of a space, or swap spaces with another Zone-deck. These proposals are evaluated by a Design Review agent and the first, if any, that improves the overall arrangement design as expressed in equation (10) is accepted. The Design Agents work on a small population of candidate designs.

The agent approach also uses I space Design Agents that simultaneously and sequentially propose changes to randomly selected candidate designs that will improve their own part of the cost function; i.e., min

. The space agents can propose to move to a new Zone-deck or swap places with a space in another Zone-deck. These proposals are evaluated by the Design Review agent and the first, if any, that improves the overall arrangement design as expressed in equation (10) is accepted.
In the agent-based approach, the agents can only improve what is already present in the current small population of candidate designs, which is initialized using a random assignment algorithm. Some form of global or divergent search is also needed for maximum performance. Combining the agents with a Genetic Algorithm Agent using mutation, crossover, and two space swap elements for a divergent search capability yielded solutions with superior overall utility (Daniels and Parsons, 2006; Daniels and Parsons, 2007). A population of 10 candidate designs was used. The hybrid agent GA solutions were superior to those obtained by either a pure GA or pure agent solution and were also significantly faster than obtained with a complex GA.

The topology optimization was performed with a conventional Genetic Algorithm using roulette selection, crossover, and two space swapping (Nick and Parsons, 2007). Using a population of four topology chromosomes and generating four stochastically-generated geometries for each topology, the GA operating for 25 generations produced an 8% improvement (Figure 8) over the best of the initial random topologies.

The example vessel presented here is an artificial demonstration design designated the Habitability Ship. It has its origins in a non-U.S. Navy 3150 tonne, 109 m Notional Corvette design. This was a two-gender design using an Officer, PO, and Specialist (enlisted) nomenclature. Because there is publication sensitivity associated with this design and with the default constraints associated with the combat related spaces, the ship was reduced for demonstration purposes to just contain the propulsion and habitability aspects of the original design. All combat spaces, one superstructure deck, and six vertical WT zones were eliminated from the vessel and the hull form was scaled to enclose this reduced size. One engine room was eliminated. The net result is a vessel with an abnormally large fraction devoted to habitability spaces.

The Habitability Ship is shown schematically in Fig. 10. There are Port (P), Center (C), and Starboard (S) Sub-Zone-decks created by the main passageways on the after part of the Damage Control Deck. The design consists of 103 spaces, 14 of which were

fixed including the bridge, bridge-related electrical equipment rooms (2), steering gear (2), anchoring and mooring, mooring area and gear storerooms (3), enclosed Rigid Inflatable Boat (RIB) stowage area, boat gear locker, main machinery room (2 levels) and auxiliary machinery room. This leaves 89 spaces to be allocated to 29 Zone-decks and Sub-Zone-decks. There were a total of 1307 goals and constraints.

The allocation for the Habitability Ship was optimized using a population of 10 candidate allocations for 1500 generations. A generation here is one round of GA operations and one cycle of space and Zone-deck agent proposals that can produce up to 5 changes each. The best solution was reached in 181 generations. This required about 20 minutes on a 2 GHz Intel Pentium Mobile PC with 1 GB RAM. No further improvement was found out to 1500 generations. In general, the arrangement is very good with a total Utility of U = 0.778. This is composed of the three component terms in equation (10) with a minimum Zone-deck area utilization utility

= 0.987, average Zone-deck area utilization utility

= 0.999, and weighted average minimum space utility

= 0.790. The

value characterizes the amount of compromise necessary for a solution. The resulting allocation of spaces is shown schematically in Figure 11 (Parsons et al., 2009).

In the automotive and consumer products industries (powered hand tools, etc.), there is a strong interest in using common base platforms for various design variants that are offered in order to save development and production costs. Methods have been in development to optimize these decisions (e.g. Gonzalez-Zugasti et al., 2000; Simpson et al., 2001; Fujita and Yoshida, 2004; Fellini et al., 2005; Fellini et al., 2006). Simpson (2004) provides an extensive review of this work.

The overall goal of the final research to be reviewed here (Corl, 2007; Corl et al., 2007a; Corl et al. 2007b) was to apply these ideas to determining the optimum commonality to use in multiple classes of ships. This involved the extension of these methods to a multicriterion approach using evolutionary optimization methods. The methodology was tested using the missions of the U. S. Coast Guard Deepwater High and Medium Endurance fleets (U.S.C.G., 1995). The design criteria were the mission performance/cost for the high endurance cutter, the mission performance/cost for the medium endurance cutter, and the fleet-wide saving from the use of commonality. The strategic design question is how much commonality to use to maximize savings without excessive degradation of the performance/cost of the two design variants.

The test application was to utilize the missions of the U.S. Coast Guard’s Deepwater Cutter fleet that consists of the Maritime Security Cutter Large (WMSL), formerly the National Security Cutter (NSC), and the Maritime Security Cutter Medium (WMSM), formerly known as the Offshore Patrol Cutter (OPC). The first NSC was launched in September 2007 and the OPC was being redesigned at the time of this work. Table 6 shows the actual design characteristics of these two designs for reference (U.S.C.G. website 2006).

The first two criteria are written as a benefit/cost ratio so that any over-design caused by the use of commonality will be penalized as wasteful. Independent variable vectors

and

defined the NSC mission vessel design and the OPC mission vessel design, respectively. Vector

defines the common components used in these designs.

The vessel designs were developed using an adaptation of the U.S. Coast Guard’s Performance Based Cost Model (NSWC, Carderock Division, 1998), which was developed by the U.S. Navy using components of its Advanced Surface Ship Evaluation Tool (ASSET, 2005) and the Canadian equivalent SHOP5 with Cost Estimating Relationships (CER’s) in constant 1998 U.S. dollars based upon the U.S. Coast Guard’s WHEC 378, WMEC 270, WMEC 210, and Great Lakes Icebreaker. The model is capable of synthesizing frigate-sized, deepwater cutters of over 1500 t including acquisition, operational, and support costs. The engines and ship service generators come from catalogs of available designs. This model was modified to reduce the number of inputs to the eight as listed in Table 7 with all needed constraints included internal to the synthesis. For example, the GMT was estimated using the parametric models from Parsons (2003)

The independent variables in Table 7 compose

and

describing the NSC mission vessel and the OPC mission vessel, respectively. The ranges considered for these variables were roughly ±10% from the values for the actual NSC and the OPC designs. The power plants considered were (1) a four (two cruise, two sprint) diesel engine CODAD plant or (2) a two cruise diesel, one spint gas turbine (CODOG) plant, with both using twin screws, mechanical gearing, and controllable pitch propellers. The weapon suites were (W1) a 46mm gun, (W2) a 57mm gun, and (W3) both a 57mm gun and a Phalanx Close in Weapon System (CIWS).

The vessel performance used a modeling similar to Brown and Salcedo (2003) who presented a multicriterion optimization methodology for mission performance versus cost. Following their model for mission effectiveness, the mission performance/cost for vessel i was as follows:

where the

are the mission profile percent time each vessel will spend in mission j. The ability of each ship i to successfully accomplish each mission j is assumed to depend upon K performance characteristics,

. The contribution of each performance characteristic yk of ship i to the success of its mission j is characterized by a fuzzy membership function or fuzzy utility

. The overall mission effectiveness is obtained by minimum correlation inference (Kosko, 1992). The Costi is the average cost of ship i.

The missions of the types of vessels were taken from U.S. Coast Guard planning (U.S.C.G., 1995). The NSC and OPC missions both include National Defense, drug interdiction, and living marine resources (LMR) missions. The NSC also performs general defense operations while the OPC performs alien migration interdiction operations.

For each of the J = 4 missions, four ship attributes were selected to describe each ship’s ability to perform these missions. The K = 4 attributes were maximum speed (knots), number of helicopter hangers (1 or 2), weapons systems, and endurance range (nm). For each mission, four fuzzy utility functions were developed for methodology testing. Those for the drug interdiction missions are shown in Fig. 12. This mission places a premium on fast aerial assets for surveillance with less emphasis on weapon systems as shown. Endurance is relatively less important in the Caribbean where most of these operations occur.

The net fleet savings function

should consider all net fleet-wide savings realized from the use of commonality through savings in training, logistical support, bulk procurement, detailed design development, and construction, etc. In this study, only the savings from bulk purchase savings and construction learning curve savings were included.

The Optimization Methodology

The commonality decisions are a set of integers in

that specify which ship components will be common between both ship classes. If a given component is designated as common, both ships are constrained to use that component. By varying the number and option choice of the common components, the design space can be populated. The various combinations of these common components are used to determine which set of common components result in Pareto optimal designs for Ship A (NSC mission) and Ship B (OPC mission). As the various combinations of commonality are applied to the designs, the optimization fills out the three criterion Pareto front or Pareto surface. Figure 13 shows a schematic of the expected discrete Pareto front that will be obtained for this multicriterion optimization.

Every set of commonality components ℓ will result in a solution for Ship

and Ship

that will be located on a line of commonality. If a single ship were being considered for both missions, this line would be the two-objective Pareto Front for Ship

performance/cost and Ship

performance/cost. For specific commonalities, Ships

and

might use the same cruise engines; Ships

and

might share the same cruise engines and weapon system. As more things become common, the savings can increase and the ship designs will tend toward each other on the Pareto surface as more effectiveness is sacrificed for commonality. When every item on the ships is common, the result will be one design for both missions (point C in Fig 13). Once every combination of common components is used in the optimization, the discrete Pareto front will be fully populated. The Pareto Front will not be continuous because of the discrete nature of the commonality variable. Rather, the Pareto front will be a collection of pairs of discrete points as shown in Fig. 13.

The optimization was performed with an adaptation of the evolutionary algorithm developed by Zalek (2007). Penalty functions for constraint satisfaction were not needed since all constraints were implemented within the synthesis model. The non-domination solution sorting was performed first for the primary criteria only and then for the sum of the primary criteria and a diversity measure D, if neither solution was dominant. This caused the method to emphasize developing non-dominated solutions early in the generations and then focus more on filling out the Pareto front through diversity pressure as the generations evolved. For testing, this was applied to the two criterion optimization of one ship design to satisfy both the NSC mission and the OPC mission. The typical progression of these solutions through 108 generations is shown in Fig. 14. The dense line through the center of the figure is the dividing line between designs with one helicopter hanger (below and to the right, the less capable OPC end) and two helicopter hangers (above and to the left, the more demanding NSC end).

The two criterion analysis for a single design to do both missions was studied to establish which choices of weapons, cruise engines, and ship service generators occurred in the Pareto optimal designs. This was used to guide which options to include in the commonality study. The results showed that only two cruise engines (C7 or C9 from the synthesis model catalog of engines), three ship service generators (G0, G1, or G3), and two weapon systems (W1 or W3) were ever Pareto optimal as shown in Fig. 15. These cruise engine and ship service generator results were used to reduce the scope of the commonality study. It was also noticed that when the number of helicopter hangers was set, there was very little variation in the resulting superstructure volume. It was with either a small superstructure (one helicopter hanger) or a large superstructure (two helicopter hangers). Also, the number of helicopter hangers resulted in little variation in the beam and depth of the hull, with either a small beam and depth or a larger beam and depth. Thus, a common superstructure (small or large) and common midship section hull blocks (small or large) were included as commonality options.

The modeling for the commonality was then an integer vector of the form

where the positions indicate the commonality decision for weapons, ship service generators, cruise engines, superstructure, and midship section hull blocks, respectively; the zero indicates no commonality is imposed; and a non-zero entry indicates the index number of the commonality choice imposed on the designs.

The multicriterion evolutionary algorithm was adapted further to obtain two separate, higher-quality solutions near the end of the

and

Pareto front, since the end points were all that was needed as shown in Fig. 13. The analysis was then run for all 288 possible combinations of commonality decisions. These results produced three bands of similar designs: 128 NSC mission vessels with two helicopter hangers, 160 NSC mission vessels with one helicopter hanger, and 288 OPC mission vessels with one helicopter hanger. Of these results, 129 of the pairs resulted in negative net fleet savings when more expensive components were being imposed on the less demanding OPC mission vessels. This is a common fallacy of most of previous work on platforms where it is usually assumed that all commonality is good. Because the optimization criterion used here involves performance/cost and no increase in the performance utilities occurs with more than the goal level, over-design results in a loss in performance/cost.

When the 159 remaining positive net fleet savings commonality pairs were sorted to determine those non-dominated designs that lie on the Pareto surface, only 20 different commonality combinations remained. Of these there were only 12 uniquely different design pairs from a naval architectural standpoint. These are as shown in Fig. 16 with the baseline, no commonality designs that yield no net fleet savings (best NSC, and best OPC). The design pair

and

(using the 46 mm gun, the smaller cruise engines, the smallest ship service generators, the small superstructure and the small midship section blocks in common) yield the greatest overall fleet savings from their commonality. Note, however, that the

design has a significant performance loss compared to the baseline design, primarily from to its use of only one helicopter hanger. The

and

designs (using the smallest ship service generators and the large superstructure in common) have the largest net fleet savings before the shift from two helicopter hangers to one. Thus, they are at a “knee” of the surface and are particularly attractive designs.

The characteristics of the

pair and the

pair of designs are shown in Table 8. Note that the NSC15 design has a significant (52.4%) performance loss compared to the baseline design, primarily due to its use of only one helicopter hanger. Note also that the two 15 designs are probably close enough that it might be better to produce one design for both missions and save even more by complete commonality. Note that the NSC18/OPC18 pair provide 97% of the NSC baseline performance, 100% of the OPC baseline performance, and still provide 60.7% of the maximum net fleet savings observed.

Three recent advanced ship design research efforts at the University of Michigan were reviewed to illustrate some of the capability of modern evolutionary and fuzzy optimization to address complex, multicriterion naval ship design problems encountered in early design. The work of Zalek used a multicriterion evolutionary algorithm to optimize the hull form of a naval combatant for smooth water powering and seakeeping performance. The work of Nick and Daniels used single criterion fuzzy optimization with either a hybrid agent/GA method or a GA to optimally allocate spaces to Zone-decks and then arrange these spaces in a naval surface vessel. The work of Corl used a multicriterion evolutionary algorithm to optimize the commonality to use in vessels for two different missions in order to maximize the net fleet savings from the commonality. Extensive references are provided to aid those interested in investigating this work further.

The optimal hull form and optimal general arrangement projects described here were sponsored by the U. S. Navy, Office of Naval Research through Luise Couchman and Kelly Cooper as part of the Naval Engineering Modeling and Optimization (NEMO) program. The optimal arrangements project was also sponsored by the U.S. Navy, Naval Surface Warfare Center Carderock Division through Robert Ames. The optimal commonality research was sponsored by the U. S. Coast Guard and the U.S. Navy, Office of Naval Research through Kelly Cooper. These efforts could not have been undertaken without this support. Special acknowledgement and thanks go to my four graduate students Stephen Zalek, Eleanor Nick, Anthony Daniels, and LCDR Michael Corl, U.S.C.G. whose graduate research is described here. Richard B. Couch Professor of Naval Architecture and Marine Engineering Robert F. Beck co-chaired Zalek’s dissertation with the author.

PARSONS, M. G., AND SCOTT, R. L. (2004). “Formulation of Multicriterion Design Optimization Problems for Solution with Scalar Numerical Optimization Methods.” Journal of Ship Research, 48:1, March.

PARETO, V. (1906). Manuale di Economica Politica. Societa Editrice Libraria, Milano, IT, also in Manual of Political Economy, The MacMillan Press Ltd. 1971.

STATNIKOV, R. B. (1999). Multicritria Design: Optimization and Identification. Dordrecht: Kluwer Academic Publishers.

COLEY, D. A. (1999). An Introduction to Genetic Algorithms for Scientist and Engineers. Singapore: World Scientific.

DEB, K. (2001). Multi-Objective Optimization using Evolutionary Algorithms. New York: John Wiley & Sons.

GEN, M. AND CHANG, R. (2000). Genetic Algorithms and Engineering Optimization. New York: Wiley Interscience.

GOLDBERG, D. E. (1983). “Computer Aided Gasline Operation using Genetic Algorithms and Rule Learning.” Ph.D. Dissertation, University of Michigan.

GOLDBERG, D.E. (1989). Genetic Algorithms for Search, Optimization, and Machine Learning. Reading, MA: Addison-Wesley.

HOLLAND, J. (1975), Adaptation in Natural and Artificial Systems. Ann Arbor: University of Michigan Press and (1992) Cambridge: MIT Press.

LI, J., AND PARSONS, M. G. (2001). "Complete Design of Fuzzy Systems using a Real-Coded Genetic Algorithm with Imbedded Constraints." Journal of Intelligent and Fuzzy Systems, 10:1.

MICHALEWICZ, Z. (1996). Genetic Algorithms + Data Structures = Evolutionary Programs. Berlin: Springer-Verlag.

OSYCZKA, A. (2002). Evolutionary Algorithms for Single and Multicriteria Design Optimization. Berlin: Physica-Verlag.

ZITZLER, E., LAUMANNS, M. AND BLEULER, S. (2003). “A Tutorial on Evolutionary Multi-objective Optimization.” http://citeseer.ist.psu.edu/zitzler03tutorial.html.

BROWN, A. AND SALCEDO, J. (2003). “Multiple-objective Optimization in Naval Ship Design.” Naval Engineers Journal, 115:4,49-61.

KOSKO, B. (1992). Neural Networks and Fuzzy Systems: A Dynamical Systems Approach to Machine Learning. Englewood Cliffs, NJ: Prentice-Hall.

LI, J. AND PARSONS, M. G. (1998). “An Improved Method for Shipbuilding Market Modeling and Forecasting.” Transactions of the Society of Naval Architects and Marine Engineers, 106:157-183.

MENDEL, J. M. (2001). Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions. Upper Saddle River, NJ: Prentice Hall PTR

SAATY, T. L. (1996). The Analytical Hierarchy Process. Pittsburgh: RWS Publishing.

ZADEH, L. (1965). “Fuzzy Sets.” Information and Control, 8:338-353.

ZIMMERMAN, H.-J. (1991). Fuzzy Set Theory – and Its Applications. 2nd Ed. Boston: Kluwer Academic.

ASSET (2005). “Advanced Surface Ship Evaluation Tool.” Version 5.2.0, Naval Surface Warfare Center, Carderock Division.

BECK, R. F. AND TROESCH, A. W. (1989). “SHIPMO.BM User’s Manual.” University of Michigan, Department of Naval Architecture and Marine Engineering. Report No. 89-2.

HIMENO, Y. (1981). “Prediction of Ship Roll Damping – State of the Art.” University of Michigan, Department of Naval Architecture and Marine Engineering. Report No. 239.

HOLTROP, J. (1984). “A Statistical Re-analysis of Resistance and Propulsion Data.” International Shipbuilding Progress, 31:363, 272-276.

HOLTROP, J. AND MENNEN, G. G. J. (1982). “An Approximated Power Prediction Method.” International Shipbuilding Progress, 29:335, 166-170.

PARSONS, M. G., LI, J. AND SINGER, D. J. (1998). “Michigan Conceptual Ship Design Software Environment User’s Manual.” University of Michigan, Department of Naval Architecture and Marine Engineering. Report No. 338.

KEANE, R. AND SANDBERG, W. C. (1984). “Naval Architecture of Combatants: A Technological Survey.” Naval Engineers Journal. 92.

ZALEK, S. F. (2007). “Multicriterion Evolutionary Optimization of Ship Hull Forms for Propulsion and Seakeeping.” Ph.D. Dissertation. Naval Architecture and Marine Engineering, University of Michigan. January.

ZALEK, S. F., PARSONS, M. G. AND PAPALAMBROS, P. Y. (2006a). “Multi-Criteria Design Optimization of Monohull Vessels for Propulsion and Seakeeping.” Proceedings of the 9th International Marine Design Conference. Ann Arbor, MI. 2:533-557.

ZALEK, S. F., PARSONS, M. G. AND BECK, R. F. (2006b). “Evolutionary Multicriterion Optimization for Propulsion and Seakeeping.” Proceedings of the 26th Symposium on Naval Hydrodynamics. Rome, IT. 2:69-85.

ZALEK, S. F., BECK, R. F. AND PARSONS, M. G. (2008). “Nonlinear Hull Form Transformation for Use with Design Optimization.” Summer Computer Simulation Conference. Edinburgh, UK. June.

ZALEK, S. F., PARSONS, M. G. AND BECK, R. F. (2009). “Naval Hull Form Multicriterion Hydrodynamic Optimization for the Conceptual Design Phase.” to appear in Journal of Ship Research.

DANIELS, A. AND PARSONS, M. G. (2006). “An Agent-based Approach to Space Allocation in General Arrangements.” Proceedings of the 9th International Marine Design Conference. Ann Arbor, MI. 2:673-695.

DANIELS, A. AND PARSONS, M. G. (2007). “Development of a Hybrid Agent-Genetic Algorithm Approach to General Arrangements.” Proceedings of the 4th International Conference on Computer Applications and Information Technology in the Marine Industries (COMPIT'2007). Cortona, IT, April.

DANIELS, A. AND PARSONS, M. G. (2008). “Development of a Hybrid Agent-Genetic Algorithm Approach to General Arrangements.” Ship Technology Research (Schifftechnik), 55.

LEAPS (2006). “Leading Edge Architecture for Prototyping Systems.” Version 3.4. Naval Surface Warfare Center, Carderock Division.

NICK, E. (2008). “Fuzzy Optimal Allocation and Arrangement of Spaces to Zone-decks in Naval Surface Ship Design.” Ph.D. Dissertation. Naval Architecture and Marine Engineering, University of Michigan. April.

NICK, E. AND PARSONS, M. G. (2007) “Fuzzy Optimal Arrangement of Spaces within a Zone-deck Region of a Ship.” Proceedings of PRADS 2007. Houston, TX.

NICK, E., PARSONS, M. G. AND NEHRLING, B. (2006). “Fuzzy Optimal Allocation of Spaces to Zone-decks in General Arrangements.” Proceedings of the 9th International Marine Design Conference. Ann Arbor, MI. 2:651-671.

PARSONS, M., CHUNG, H., NICK, E., DANIELS, A., LIU, S. AND PATEL, J. (2009). “Intelligent Ship Arrangements (ISA): a New Approach to General Arrangement.” to appear in Naval Engineers Journal.

CORL, M. J. (2007). “Methodology for Optimizing Commonality Decisions in Multiple Classes of Ships.” Ph.D. Dissertation. Naval Architecture and Marine Engineering, University of Michigan. June.

CORL, M. J., KOKKOLARAS, M. AND PARSONS, M. G. (2007a). “Platform-Based Design of a Family of Ships Considering both Performance and Savings.” Proceedings of the International Conference on Engineering Design, ICED'07. Paris, France. August 28-31.

CORL, M. J., PARSONS, M. G., AND KOKKOLARAS, M. (2007b). “Methodology for the Optimization of Commonality in Multiple Ship Classes.” Transactions of the Society of Naval Architects and Marine Engineers. 115: 68-93.

FELLINI, R., KOKKOLARAS, M., PAPALAMBROS, P. Y. AND PEREZ-DUARTE, A. (2005). “Platform Selection under Performance Loss Constraints in Optimal Design of Product Families.” Journal of Mechanical Design, 127:4: 524-535.

FELLINI, R., KOKKOLARAS, M. AND PAPALAMBROS, P. Y. (2006). “Quantitative Platform Selection in Optimal Design of Product Families, with Application to Automotive Engine Design.” Journal of Engineering Design, 17:5: 429-446.

FUJITA, K. AND YOSHIDA, H. (2004). “Product Variety Optimization: Simultaneously Designing Module Combination and Module Attributes.” Concurrent Engineering: Research and Applications. 12:2: 105-118
GONZALEZ-ZUGASTI, J.P., OTTO, K. N. AND BAKER, J. D. (2000). “A Method for Architecting Product Platforms.” Research in Engineering Design, 12: 61-72.

NAVAL SURFACE WARFARE CENTER CARDEROCK DIVISION (1998). “User’s Guide USCG Performance Based Cost Model.”
PARSONS, M. G. (2003). “Parametric Design.” Ch. 11 in Ship Design and Construction, I, T. Lamb (ed.), New York: Society of Naval Architects and Marine Engineers.

SIMPSON, T.W. (2004). “Product Platform Design and Customization: Status and Promise.” Artificial Intelligence for Engineering Design, Analysis, and Manufacturing. 18: 3-20.

SIMPSON, T.W., MAIER, J. R. A. AND MISTREE, F. (2001). “Product Platform Design: Method and Application.” n, 13: 2-22.
U.S. COAST GUARD MEMORANDUM (1995). “Mission Analysis Report (MAR) N-001-95 Deepwater Missions.”