Fuzzy Predictive Model of the Vertical Acceleration of a High Speed Vessel in Pitch Motion

Francisco Gil Navia¹
Juan Contreras Montes²

Abstract

An adaptable fuzzy inference technique is being described in order to generate predictive models of the acceleration of the pitching of a high speed vessel, from the data obtained from the web on an experiment conducted by the University of Iowa. The geometry of interest in the experiment is a scale model of the type 1/46.6 of the DTMB model 5415 (DDG-51). The fuzzy algorithm for the generation of the predictive model uses a triangular partition with a 0.5 overlapping and consequents of the Singleton type. The consequents are adjusted in an automatic fashion by using recursive least squares. The algorithm shows a very low computational complexity rate which allows for it to be used for on line identification.

Key words: fuzzy identification, vessel pitching, fuzzy predictive model, recursive least squares.

Resumen

Se describe una técnica de inferencia borrosa adaptativa para generar modelos predictivos de la aceleración de cabeceo de un buque de alta velocidad, a partir de datos obtenidos de la web de un experimento realizado en la Universidad de Iowa. En el experimento, la geometría de interés es un modelo a escala 1/46.6 del DTMB modelo 5415 (DDG-51). El algoritmo borroso para la generación del modelo predictivo emplea partición triangular con solapamiento de 0.5 y consecuentes tipo singlenton. Los consecuentes son ajustados de manera automática empleando mínimos cuadrados recursivos. El algoritmo presenta una baja complejidad computacional lo que permite su empleo para identificación en línea.

Palabras claves: identificación borrosa, cabeceo de buque, modelo predictivo borroso, mínimos cuadrados
recursivos.

Date received: March 2nd, 2009 - Fecha de recepción: 2 de Marzo de 2009
Date Accepted: October 19th, 2009 - Fecha de aceptación: 19 de Octubre de 2009

________________________

¹ Escuela Naval Almirante Padilla. Facultad de Ingeniería Naval. Cartagena de Indias, Colombia. e-mail: negrogil@hotmail.com
² Escuela Naval Almirante Padilla. Facultad de Ingeniería Naval. Cartagena de Indias, Colombia. e-mail: epcontrerasj@ieee.org

............................................................................................................................................................

Introduction

Thanks to the current use of lighter materials in the construction of vessels great growth has been achieved in the development of high speed vessels. However, the high speeds that have been achieved generate in turn vertical accelerations which result in dizziness and fatigue for the members of the crew and to the passengers as well, thus affecting the safety and comfort. In order to get a decrease in vertical accelerations, control surfaces are used in high speed vessels which through the appropriate control system vary the attacking angle presented by the ocean in its advance, thus generating a reaction to the vertical forces actuating upon the ship. (Santos et al, 2005).

To design the pitching control system it is necessary to have a model capable of predicting the vertical acceleration value from the previous data taken from the input variables related to the dynamics of the waves. Modeling complexity is due to the fact that we are dealing with a dynamic that is highly non - linear.

Fuzzy logics have proven to be greatly useful to represent the behavior or dynamics of the systems through diffuse rules of the IF-THEN type. The first systems that were based on diffuse rules were supported on the information as supplied by an expert; however, in the case of complex systems the rules that had been built that way did not allow for an acceptable simulation of the system. In the search of fuzzy systems that approximate in an acceptable manner the dynamics of complex systems has lead to the development of a research in extraction techniques of fuzzy rules from the input and output data; that is, the development of fuzzy identification techniques (Sugeno and Yasukawa, 1993).

One of the first proposals for the automatic design of fuzzy systems from experimental data is the technique called the look-up table scheme (Wang and Mendel, 1992). Other important methods use the descending gradient, grouping or clustering techniques and evolutionary algorithms. Except for the last one, all methods require a previous design of the membership functions.

Building a fuzzy model requires the selection of a great number of parameters: number, form and distribution of the membership functions, construction of the rule base, selecting the logical operators, selecting the inference method, among others. All these needs for a systematic criterion to be applied in order to make an accurate selection (Espinosa and Vandewalle, 2000).

Fuzzy cluster algorithms represent the most appropriate technique to obtain fuzzy models. The Fuzzy C-Means (Bezdek, 1987) and Gustafson-Kessel (1979) methods are the most used ones. Several variations have been done to these cluster algorithms. Nauck and Kruse (1995, 1999) suggest neuro- diffuse cluster techniques; Espinosa and Vandewalle (2000) present a methodology to extract rules from the data within a linguistic integrity frame including fusion algorithms to group sets whose modal values are at a very close distance. Sala (1998, 2001) introduces a novel technique based on the inference error to approximate functions by using partition sum1 with triangular sets; Díez et al (2004) propose introducing variations to the cluster algorithms in order to improve the ability to interpret them and find local structures that are similar within the fuzzy models obtained. Paiva and Dourado (2004) present a model that has been generated through the training of a neuro- diffuse network which was implemented in two phases: during the first phase, the structure of the model is obtained by using a subtractive clustering algorithm, which allows for the extraction of the rules from input and output data; during the second phase, the parameters of the model are tuned in by means of a neural network that uses back propagation. Guillaume and Charnomordic (2004) propose a strategy to generate interpretable diffuse partitions from the data in which they incorporate an algorithm they call hierarchic fuzzy partition (HFP) which adds fuzzy sets instead of incorporating data in each iteration. They also present a fusion algorithm of the fuzzy sets based on the appropriate metrics that ensure semantic interpretability.

The methodology used in this paper to obtain the fuzzy model from the input and output data is based on Sala’s (1998) error inference method and is presented in three phases: during the first phase, the inference error is used to detect possible types or clusters within the data; during the second phase, rules are generated; during the third one the form, number and distribution of the fuzzy sets are generated. Using an ideal inference method is another proposal that has been made.

Characteristics of the Data Collection Experiment

The following study is supported on the work done by Irving et al (2006), on the experimental tests carried out at the test tank of IIHR (Hydro science & Engineering from the University of Iowa, Iowa City, USA) using a DTMB (David Taylor Model Basin) a 5512, as the geometry of interest. The data was taken from the following web page: (http://www.iihr.uiowa.edu/~shiphydro/efd_vdata_5512_pitch_and_heave.htm).

The tests are carried out in the test tank at Iowa University IIHR. The tank has 100 m of length, a width equivalent to 3.048m and a depth of 3.048m and it is equipped with a wave generator of the automated plunger type. The towing car is equipped with 2 data acquisition computers, circuit speed and signal conditioning to measure analog voltages measured from the speed of the vessel, speed of the carriage and wave elevation.

The geometry of model 5512 scale 1:46.6 with Lpp=3.048m is made of reinforced fiber with CB=0.506. This model is a symmetrical geometric scale (geosim) of the DTMB 5415 (scale 1:24.8, Lpp=5.72m), that has been conceived by the US Navy as a preliminary design of a combatant.

The tests are conducted for 5 Froude Numbers Fr and 3 wave steepnesses Ak, where

from where:
Uc = speed of the towing carriage
A = wave amplitude
Fr = 0.28 corresponds to the cruising speed
Fe = wavelength

Data collection occurs at 80, 106.7, 160 Hz / channel, for 30, 20, 15, 10 seconds correspondingly, for those cases where Fr = 0.19, 0.28, 0.34, 0.41, correspondingly. The parameters for the collection of data are the same for Fr = 0 and 0.19, Uc = 0 m/s. The data includes ballasting parameters, the encounter frequency, time histories, Fourier series amplitudes and pitch and heave transfer functions and phase.

Fuzzy Modeling Algorithm

The algorithm for fuzzy systems that can be interpreted from the data available is based on minimization process of the inference error. All the user needs to do is to introduce the data of the input and output variables. The algorithm determines the ranges of each variable, distributes the membership functions within the universes of each input variable, locates the consequents of the Singleton type in the outlet space, determines the rules and adjusts the location of the consequents, by using the least squares in order to minimize the approximation error. The algorithm stops once it has an error measurement that is lower than the one required by the user or when the number of fuzzy sets per input variable is greater than 9. The distribution of the membership functions in each input universe is done in a uniform fashion in order to guarantee that the resulting partition is sum 1; that is, the sum of all the degrees of membership of a data within an input variable will always be equal to 1 (Gil and Contreras, 2008).

Given a collection of experimental input and output data , with i = 1...N; k = 1..., p, where is the input vector of input p-dimensional is the output one dimensional vector.

1. Organization of the set of N pairs of pieces of input - output data , where are input vectors and are output scaling.
2. Determining the ranges of the universes of each variable as per the maximum and minimum values of the data associated [xi-, xi+], [y-, y+]
3. Distribution of the triangular membership functions on each universe. As a general condition the vertex with a membership value of one (modal value) falls in the center of the region that is covered by the membership function while the other two apexes, with a membership value equal to zero, fall in the center of the two neighboring regions. In order to be able to efficiently approximate the lower and upper ends of a function that is being represented by the data it is necessary for the membership functions covering the beginning and end of the universe that in the triangular partition to coincide their apexes with their membership values of one with their left and right apexes correspondingly, as shown in Fig. 1.

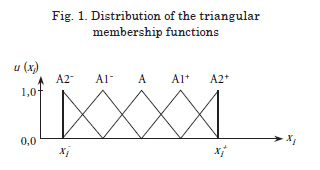
Calculating the position of the modal values of the input variable (s), as per the following:

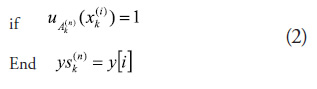
where corresponds to the projection on the outlet space of the assessment of data de la k-th input variable in the n-th corresponding partition set. The value of the output that corresponds to the said projection is given by the value of the i-th position of the output vector y.

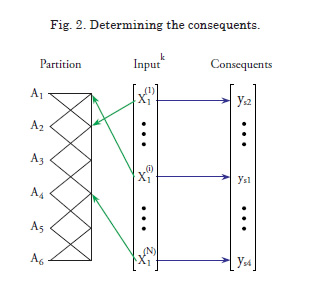
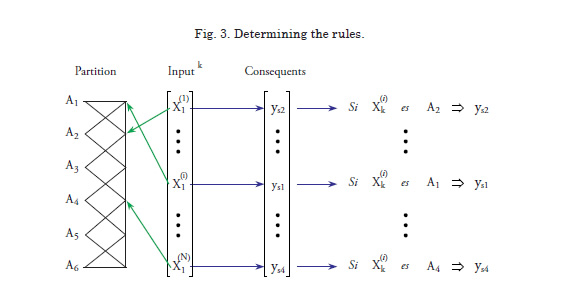
5. Determining the rules. The number of rules as initially obtained is the same as the number of sets of each input variable multiplied by the number of variables; that is, it is equal to n × k. The membership functions associated to each consequent will form the antecedents of the rules. An algorithm to reduce the number of rules will be introduced later on. (see Fig. 3)

6. Validation of the model, or calculating the approximation by using the inference method as described by where is the solitary value that corresponds to rule j

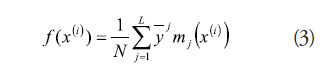
7. Adjusting the parameters by relocating the output solitaires, using the least squares method. In order for that to be possible, the equation (2) is presented as

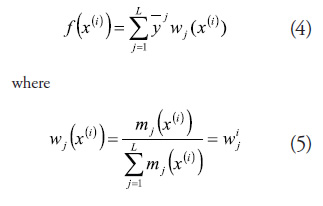
As per the inference process, the output n values may be represented with the form , which in a matrix form is given by

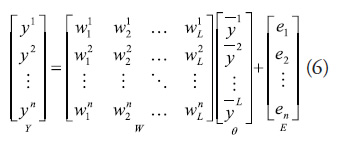
where E is the approximation error that has to be minimized, and is the consequent vector.

When using the norm of the root square error we have

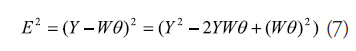
The solution to this least squares problem, by adjusting the consequents, is given by

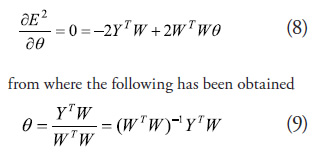
This solution is valid if is not singular, what this means is that all the rules need to receive sufficient excitation (persistent excitation) during training. This is not always possible in practice, which is why it is recommended to go to the application of recursive least squares, seeking to guarantee that the adaptation process will affect the rules that have been excited (Contreras, 2006; Espinosa and Vandewalle, 2000, 2005).

8. Determine whether the measurement of the root mean square error MSE is lower than a measurement that has been previously established. Otherwise, increase in 1 the number of sets of the income variable and go back to step 3.

With the method that has been proposed it is possible to obtain a fuzzy model that can be interpreted with some degree of accuracy and the only thing needed is to adjust the parameters of the consequent, which are of the solitary type. This results in a decrease of the training time. It is possible to achieve a greater approximation (“fine adjustment”) if upon finalizing the said process the decreasing gradient method were to be applied only to adjust the location of the modal values of the triangular sets of the antecedent, keeping the partition sum 1 and, therefore the interpretation ability of the system.

Results

The suggested method was applied to the experimental data found on the web page of the University of Iowa (http://www.iihr.uiowa.edu/~shiphydro/efd_vdata_5512_pitch_and_heave.htm), and that was taken from tests made to the model DTMB 5512, which is on scale of 1/46.6 of model DTMB 5415 (DDG-51) with = 3.048 m. The experiments were carried out in a towing tank that was 3 x 3 x 100 m and that was equipped with a wave generator of the plunger type. Several tests or series of tests were carried out, all of them at constant speed. The sampling speed was 53.3 samples per second. In order to obtain the model, all series were taken, regarding the wave signal at the following times: w(k-12) and w(k-6), as well as the pitch angle y(k) as input variables to predict the pitch angle at instant y(k+6).
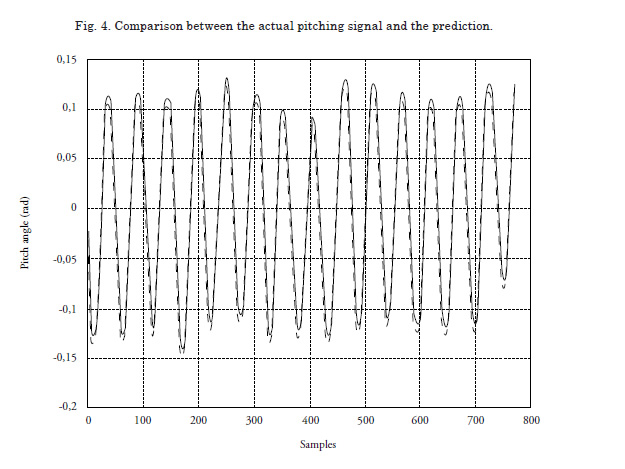
The fuzzy model that was obtained has 3 triangular sets per variable (Low, Intermediate and High) which are evenly distributed and 12 rules. 800 pieces of data were used for the identification and 800 pieces of data for validation. The root mean square error MSE reached was equivalent to 0.0012. Fig. 4 shows the comparison made between the actual process and the fuzzy model.

Conclusions

A method based on minimizing the inference error for the identification of systems from the data available is being presented here. The suggested strategy includes the use of fuzzy models that can be interpreted with the adjustment of the consequent parameters of the Singleton type, by using least squares. The method does not require the use of other artificial intelligence techniques.

Using the experimental data with a model replicated on a scale of 1/46.6 of model DTMB 5415 (DDG-51) a predictive fuzzy model has been obtained for the acceleration of the pitching.

Applying the method in the identification of classical dynamic processes has allowed for the obtainment of fuzzy models with a high accuracy rate without being forced to sacrifice the interpretation ability, as happens with most of the available methods.

References

BEZDEK J. C. Pattern recognition with Fuzzy Objective Function Algortithms. Ed. Plenum Press. 1987.

CONTRERAS, J. Introducción al Control Automático, Editorial Escuela Naval, Almirante Padilla, Cartagena, Colombia, 2006.

CONTRERAS, J., MISA, R., PAZ, J., Building Interpretable Fuzzy Systems: A New Approach to Fuzzy Modeling. En proceedings of Electronics, Robotics and Automotive Mechanics Conference

CERMA 2006. IEEE Computer Society. Pags.: 172-178. 2006.

DÍEZ J. L., NAVARRO J. L., SALA A. Algoritmos de Agrupamiento en la Identificación de Modelos Borrosos. RIAI: Revista Iberoamericana de Automática e Informática Industrial. 2004

ESPINOSA, J., VANDEWALLE, J. Constructing fuzzy models with linguistic integrity form numerical data-afreli algorithm, IEEE Trans. Fuzzy Systems, vol. 8, pp. 591 – 600. 2000.

ESPINOSA, J., VANDEWALLE, J., Wertz, V, Fuzzy Logic, Identification and Predictive Control. Springer. Estados Unidos. 2005.

GIL, F., CONTRERAS, J. Automatic tracking of Target: Application on a Prototype of Cannon. II Conferencia/Workshop de Vehículos/Sistemas No-Tripulados (UV/S) de América Latina. Panamá. Agosto de 2008.

GUILLAUME, S., CARNOMORDIC, B. Generating an interpretable Family of Fuzzy Partitions Form Data, IEEE Trans. Fuzzy Systems, vol. 12, No. 3, pp. 324 – 335. 2004.

GUZTAFSON E. E., KESSEL W. C. Fuzzy Clustering with a Fuzzy Covariance Matrix. IEEE CDC, San Diego, California, pp. 503 – 516. 1979.

IRVINE, M., LONGO, J., and STERN, F., Pitch and Heave Tests and Uncertainty Assessment for a Surface Combatant in Regular Head Waves, Journal of Ship Research, submitted. 2006.

NAUCK, D., KRUSE, R., Nefclass - a neuro-fuzzy approach for the classification of data, In: Proceedings of the Symposium on Applied Computing. 1995.

NAUCK, D., KRUSE, R. Neuro-fuzzy systems for function approximation. Fuzzy Sets and System. 101(2), pp. 261-271. 1999.

PAIVA, R. P., DOURADO, A. Interpretability and learning in neuro-fuzzy systems, Fuzzy Sets and System. 147, pp. 17-38. 2004.

SALA, A. Validación y Aproximación Funcional en Sistemas de Control Basados en Lógica Borrosa. Universidad Politécnica de Valencia. Tesis Doctoral. 1998.

SALA, A., ALBERTOS, P. Inference error minimisation: fuzzy modelling of ambiguous functions. Fuzzy Sets and Systems, 121 pp. 95 – 111. 2001.

SANTOS, M., LÓPEZ, R., de la CRUZ, J.M., Modelo predictivo neuro-borroso de la aceleración de cabeceo de un buque de alta velocidad. RIAI: Revista Iberoamericana de Automática e Informática Industrial. 2005.

SUGENO, M., YASUKAWA, T. A fuzzy logic based approach to qualitative modeling. Transactions on Fuzzy Systems, vol. 1, No. 1, pp. 7-31. 1993.

WANG, L-X, MENDEL, J.M. Generating fuzzy rules by learning form examples, IEEE Transactions on Systems Man and Cybernetics, vol. 22, no 6, pp. 1414-1427. 1992.