Rafael Arévalo Ascanio 1
Rafael Santofimio Rivera 2
Jair Eduardo Rocha González 3
Wilson Adarme Jaimes 4
1 Universidad Nacional de Colombia. Bogotá, Colombia. Email: rarevaloa@unal.edu.co
2 Universidad Nacional de Colombia. Bogotá, Colombia. Email: rasantofimior@unal.edu.co
3 Universidad Nacional de Colombia. Bogotá, Colombia. Email: jerochag@unal.edu.co
4 Universidad Nacional de Colombia. Bogotá, Colombia. Email: wadarme@unal.edu.co
Date Received: February 6th 2017 - Fecha de recepción: Febrero 6 de 2017
Date Accepted: March 3rd 2017 - Fecha de aceptación: Marzo 3 de 2017
This article considers the problem of locating multiple installations for the intermodal transport network in Colombia, and is based on the analysis of the transport of cargo from the main generating cities to the three most important port cities in the Caribbean region of the country: Barranquilla, Cartagena and Santa Marta; integrating the modes of transport by land, road and river. According to this, land transport by road is used from the source of cargo to the possible locations of the logistic platforms, and then the Magdalena River basin is used as a unique river corridor.
The model proposed consists of determining the optimal location of a series of logistic platforms that guarantee a system of integration and cooperation in transport strategies for the country, in which aggregation and disaggregation of freight operations will be possible. In this aspect, an entire mixed programming model is performed with the objective of minimizing the total costs of transport and operation of the new intermodal network, with restrictions associated with the generation and processing of cargo, obtaining results in the cost functions related to cargo transport and leaving as evidence the potential of integrating intermodal transport for the country's competitiveness.
Key words: Logistics Platform, intermodal transport, Multi-Facility localization problem.
Este artículo considera un problema de localización de instalaciones múltiples para la red de transporte intermodal en Colombia, para ello se analizó el transporte de carga desde las principales ciudades generadoras hasta las tres ciudades portuarias más importantes de la región caribe del país: Barranquilla, Cartagena y Santa Marta; integrando dos modos de transporte, terrestre por carretera y fluvial. De acuerdo a esto, el transporte terrestre por carretera se utiliza desde los orígenes de carga hasta las ubicaciones posibles de las plataformas logísticas, para luego usar como único corredor fluvial la cuenca del río Magdalena.
El modelo propuesto consiste en determinar la ubicación óptima de una serie de plataformas logísticas que garantizan un sistema de integración y cooperación en estrategias de transporte para el país, en las cuales serán posibles operaciones de agregación y de desagregación de carga. En este aspecto, se realiza un modelo de programación mixto entero con el objetivo de minimizar los costos totales de transporte y operación de la nueva red intermodal, con restricciones asociadas a la generación y procesamiento de carga, obteniendo resultados en las funciones de costos referentes al transporte de carga y dejando como evidencia el potencial que tiene la integración del transporte intermodal para la competitividad del país.
Palabras claves: Plataforma logística, transporte intermodal, problema de localización de instalaciones múltiples.
At the global level, river transport is characterized as a competitive and clean mode of transport. Costs per tonne/kilometer are low compared to other modes of transport and the carbon emissions are low (Ministry of Transport, 2015). However, the movement of cargo in the waterways of the country has not increased significantly over recent years, mainly because the freight that can be transported by rivers has been essentially absorbed by the roads (Gómez, 2012) because only 2% of the national freight is transported by fluvial means (ANDI, 2016).
Betting on an exclusive road system would mean to waste a great opportunity in building a more competitive country. An inter-modal system should be developed integrating as many modes of transport as possible. "Colombia must correct one of its biggest historical errors, abandoning river transport" (Ospina Hernández, 2008).
The strengthening of inter-modal transport is a strategy that can be developed in conjunction with public and private entities with the aim of generating greater coverage in the freight and passenger transport services at reasonable costs while ensuring continuity in the service. Currently, in Colombia, the little use of intermodal transport increases logistical costs in comparison with countries that are members of the OECD (Ministry of Transport, 2015).
According to the master Plan of Intermodal Transport PMTI (2015), three conditions are required to make it an effective means, first, an adequate functioning of each mode; second, an efficient connection between modes; and third, new knowledge in logistical development in the government and in the private sector. The latter defines the importance of the state in these types of initiatives, in which functions such as the promotion of infrastructure projects, economic regulation, stipulate financing mechanisms and articulate the different sectors with policies and planning that are fundamental to the effective development of an intermodal transport.
The problem of locating facilities investigates where to locate a set of installations in a geographic or influence area with the objective of minimizing the costs and satisfying some restrictions, including the covering of some demand points in an efficient way, contemplating the flexibility and evolution of the latter in time (Hale & Beberg, 2003).
According to literature this problem has been used in a wide variety of applications in various supply chains, which include locations of material collection centers, hazardous waste locations, stations for transportation methods, service providers, recreation facilities in cities, location of bank servers, among others, which have had different characteristics in terms of their objective function, distance metrics applied, number and size of the facilities to be located, as well as other relevant characteristics in the formulation of the problem (Hale & Beberg, 2003; Arabani & Farahani, 2011).
Currently the facility localization problem (FLP) is defined by two classical elements in this type of formulation: time and space, in which the concepts of geographical area of influence and travel times are incorporated from a new location to an existing one (Arabani & Farahani, 2011).
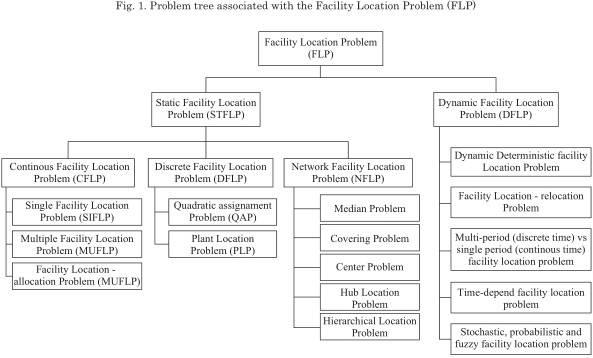
Therefore, the study of this problem currently includes multiple variants, which has caused the state of the art in this regard to present various types of problems that essentially study changes in the aspects of time, area, number of facilities and other conditions (Hale & Beberg, 2003), showing the following tree of variants of the original problem (Arabani & Farahani, 2011): see Fig. 1.
From Fig. 1, it is possible to show some of the features that identify and di fferentiate typical problems associated with the Facility Location Selection problem, as indicated in table 1, in which it is possible to see what the variations of each type of sub-problem are that belong to this kind of problem that are typical of the design of productive systems.
Usually these types of problems generally include, in the optimization of the target location, functions related to a cost and time analysis (Arabani & Farahani, 2011), where the most common are the general objective of minimizing the distance between points of the logistic network, the estimation of the minimum number of new installations and satisfaction of the demand (Hale & Moberg, 2003).
As a complement, the optimization functions available in the literature on the topic show different types of objectives available in applications that are focused on minimizing costs, distance, time and risk, maximizing profits and availability of services as well as multi-criteria objectives (Arabani & Farahani, 2011). Likewise it is possible to determine the use of exact techniques, heuristics, specific algorithms and general methods for the solution of this type of problems (Arabani & Farahani, 2011).
As for the application of this type of modeling for problem solving, in the literary review carried out by Arabani and Farahani it is possible to find different application contexts that include chemical industries, transport, schools, medical services,
electronic industries, disaster management, fire systems, military industries, production and distribution systems, the petrochemical industry, libraries, the police service and telecommunications among others (Arabani & Farahani, 2011).
Finally, in the literary review it is possible to find development proposals for the topic in which the integration and combination of dynamic models of FLP are found, for which some authors initiate a process of development to obtain more favorable results in investment decision making (Arabani & Farahani, 2011). Similarly, it is shown how localization problems can be seen from the supply chain, in international areas of collaboration and business integration.
Also from a criterion of the author it is possible to research FLP dynamic models in the conformation of supply networks in which the demands and the response times of the installations are probabilistic in nature, foreseeing in a better way the investment considerations. Another aspect in which the author suggests the work is in the implementation of FLP models in disaster management, from a perspective of dynamic models and how they develop a supply chain from these primary care sites (Arabani & Farahani, 2011).
As has been seen in the literature review there are different variants for the facility localization problem (FLP), grouped into two types: static and dynamic. For the object under study in this paper, the problems of static localization are those that best adjust given the characteristics and specific restrictions of the case. Within these are subproblems that address different aspects such as time, space, number of installations, among others; which are: Discreet Location Problems (DFLP), the Localization Problem in Network installations (NFLP) and the continuous location problem (CFLP). The latter being the one that considers the problems in which each installation is located as a point in a region on a plane and the relationship between customers and facilities is a measure of distance. (Ballou, 1968).
On the other hand, continuous location issues present some particular cases such as: SingleInstallation location problem, Service location problem and multi-facility localization problem.
The problem of locating multiple facilities is that facilities must be located so that the Euclidean or Manhattan distance, or transportation costs with other locations are the minimum possible (Akyuz, Oncan, & Altnel, 2009). In this order of ideas, this particular case allows the behavior and the interactions between the different agents that intervene in the transport of cargo in Colombia to be modelled.
Once the type of localization problem to be used has been determined, we will have as the objective the minimization of the total cost generated in the transport of a cargo unit from a point of origin to a final destination. These total costs will be disaggregated in transportation costs in two different ways and in the implementation costs of the logistics platform. In order to establish land transportation costs by road the SICE-T Transport Ministry tool is used with base prices of 2015, as for the fluvial mode, the value of the transport of one ton per kilometer is generalized from the data presented in the fluvial master plan of Colombia (2015).
For the configuration of the network three fundamental elements are defined: load-generating nodes, logistic platforms and sump nodes. As for the first element, cities were identified that generate 85% of the cargo transported to the main seaports of the Caribbean using the origin-destination matrices of the Ministry of Transport (2013). These chosen cities are Bogotá, Medellín, Cali, Villavicencio, Montería, Cúcuta, Bucaramanga and Valledupar.
Logistic platforms are intermediate network nodes that disaggregate and add load, integrating land transport modes by road and river. To select the possible locations of these platforms the main river ports on the Magdalena river are defined according to the report of the Coremar (2015) group, which are: Honda, Puerto Salgado, Puerto Berrío, Barrancabermeja, Puerto Wilches, Gamarra, El Banco, Mompós, Calamari and Barranquilla.
Finally, the sinking nodes or final destinations arise because of their location near the mouth of the Magdalena River, a river corridor involved in the intermodal network that is defined in this study. These nodes are: Cartagena, Barranquilla and Santa Marta.
As mentioned above the network under study has three main elements, Origins (i), Platform (j) and Destination (k).
Assumptions:
The parameters and variables used in the model are as follows:
Sets:
i Set of Origins (i = 1,2,3,...,I)
j Set of Platforms (j = 1,2,3,...,J)
k Set of Destinations (k = 1,2,3,...,K)
Parameters:
CTR1i,j: Cost of transport per ton of cargo between the cities of origin type i and the possible location of the logistic platform j [$/ton]
CTR2j,k: Cost of transport per ton of cargo between the logistic platforms type j and destination ports type k [$/ton]
Chj: Operating cost per year in the logistics platform type j [$/año]
Capcj: Storage and handling capacity in the logistics platform type j [Ton/year]
Decision Variables:
CT: Total cost of transport and operation of the logistic system
Xi,j: Amount of cargo to be transported between the city of origin type i and the Logistics Platform Type j [ton/year]
Yi,j: Amount of cargo to be transported between the logistic platform Type j and destination Type city k [ton/year]
Zj: 1: If the platform j comes into operation; 0: in another case
With the detailed notation above it is possible to formulate a whole mixed programming model (MIP) as follows:
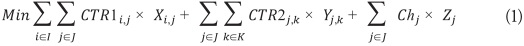
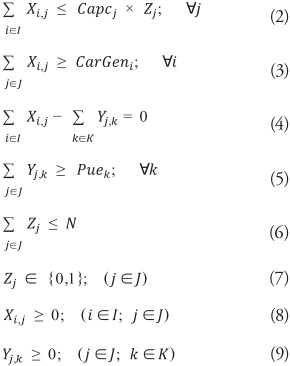
This section presents the computational results of the mathematical model developed for the problem being studies, in two different scenarios. GAMS 23.9.5 software is used to model said Issue and the Excel financial tool for submitting tables.
Initially the behavior of the system is analyzed by restricting the platform number to implement to four, in order to determine if each of these can withstand the volume generated at least in two cities. To make this possible the model is allowed to adjust the capacity of the platforms according to the requirements of cargo flows from the generating nodes.
By implementing four platforms, the river ports of Honda, Puerto Berrio, Gamarra and Calamar are activated, receiving 4,509,037, 2,041,024, 2,374,354 and 913,809 tonnes respectively, See Table 1. The cargo that arrives to Honda comes from the cities of Cali (29%), Bogotá (60%) and Villavicencio (11%), being the platform that welcomes the highest volume equivalent to 46% of total transported cargo. The provenance of the cargo that arrives to Puerto Berrio is exclusively from Medellín which represents 21% of the total transported. For its part Gamarra manages 24% of the total transported distributed from Cúcuta (48%) and Bucaramanga (52%). Finally, Calamar moves the remaining load which comes from Montería (54%) and Valledupar (46%). The costs recorded by mobilizing cargo from the generator nodes to the platforms are COP 481,852,000,000.
From the above it is evident that each platform functions as a receiving point of freight for the main regions of the country, distributed as follows:
Honda mainly receives freight from the south of the country; Puerto Berrio from the west; Gamarra from the north east zone; and Calamar from the Caribbean region. In this way It takes full advantage of the extent of the river in the national territory.
Continuing with flows from the J-platforms to the K-destinations the model gives the load distribution shown in Table 2. Th is distribution satisfies the demand requirements of each of the three major port cities in the Colombian Caribbean. Barraquilla accounts for 48% of the total of the mobilized cargo, corresponding to 4,696,840 tonnes during the year, coming from the river ports of Honda, Puerto Berrio and Gamarra. Cartagena on the other hand, receives 42% divided between Honda and Calamar. Finally, Santa Marta moves the remaining 10% of the cargo from Gamarra.
The transport costs generated by this route are calculated in COP 422,354,000,000 per year, the total cost of this operation by integrating the land and river modes ascends to COP 904,206,000,000.
On the other hand, in a second scenario where the model has autonomy to choose the optimal solution, the restriction corresponds to the platform number to implement and a theoretical capacity is established for each of them in order to prevent them from influencing the decision, taking as a criterion that these can cover at least twice the supply of the city that the higher load volume generates. This scenario shows an optimal solution in which the platforms of the previous model are maintained and includes two more as are Barrancabermeja and the same port of Barranquilla see Table 3.
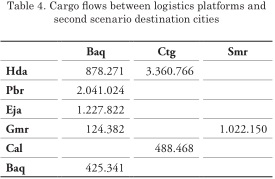
The total costs corresponding to the last segment of the network resulting from the operation of the fluvial mode are calculated in COP 434,470,000,000, an increase of 2% compared to the previous value under the same modality. Although it can be observed that river costs increased by the opening of two new platforms, this network configuration presents lower total costs. Fig. 2 graphically shows the solution found, signals the origin cities and direction of the cargo flows to each platform.
From the information collected on the previously mentioned land transportation costs and the load volumes mobilized for one year, the total annual cost of this operation has been determined using only this mode of transport, with the objective of contrasting the results that the proposed model throws.
For a year of transport only by road from the main cities generating cargo to the port cities of the Caribbean the costs rise to COP 1.73 Billion. It is clear that the implementation of the logistic platforms located in the geographical points suggested by the model represents a reduction In the costs of the order of 50% in relation to the current operation.
In Figs. 3, 4 and 5, the cost per route is detailed for origin-destination cntrasting the current operation and intermodal network settings established in the second scenario proposed.
According to the results obtained in the two modeling scenarios, it is evident that the implementation of logistic platforms at critical points significantly reduces total transport costs. In addition, the effective integration of at least two transportation modes through the logistic platforms allow the development of the intermodal network in the country.
It necessary to recover the navigability of the Magdalena river to make the implementation of an intermodal network of this type possible, in which the modes of river transport and land by road of the country are integrated. By allowing cargo transport in large volumes by this the main river corridor of the country, a resource would be exploited that is wasted right now, which as the figures indicate currently transport just 2% of the total national freight.
This work gives rise to continue researching and designing new configurations of the intermodal network that the country needs. Although here we propose specific places for the implementation of logistic platforms, it is necessary to continue validating each one of these models with new economic, social and even cultural variables, to measure more precisely the impacts that can be generate on the areas of influence.
AKYUZ, M., ONCAN, T., & ALTNEL, L. (2009). The multi-commodity capacitated multifacility Weber problem: Heuristics and confidence intervals. Proceedings of the international multiconference of engineers and computer scientist, 2.
ARABANI, A., & FARAHANI, R. (2011). Facility location dynamics: An overview of classifications and applications. Computers & Industrial Engineering, 408-420.
BALLOU, R. (1968). Dynamic warehouse location analysis. Journal of Marketing Research, 271276.
FARAHANI, R., & HEKMATFAR, M. (2009). Facility Location: Concepts, Models, Algorithms and Case studies. Berlin; Germany: Springer Verlag Berlin Heidelberrg.
GÓMEZ T, A. (2012). Strategic analysis of the shipyard Sector in Colombia: study from a Fluvial perspective. Institute of Studies for Development-IDE, University of Technology of Bolívar, Colombia.
HALE, T., & MOBERG, C. (2003). Location Science Research: A Review. Annals of Operations Research, 123(1), 21-35.
HEKMATFAR, M., & PISHVAEE, M. (2009). Hub location problem. In R. Farahani & M. Hekmatfar, Facility location: Concepts, models, algorithms and case studies (pages 243-270) BERLIN Germany: Springer Verlag Berlin Heidelberg.
MINISTRY OF TRANSPORT OF COLOMBIA (2015). Intermodal Transport Master Plan (PMTI): A State policy to make Colombia a more competitive country.
MINISTRY OF TRANSPORT OF COLOMBIA (2015). System of Information of Efficient Costs for SICE-TAC Cargo Automotive Transport. Available [www.MinistryofTransport.gov.co].
MINISTRY OF TRANSPORT OF COLOMBIA (2013). Origin-destination matrix national freight.
NATIONAL ASSOCIATION OF INDUSTRIALISTS, ANDI. (2016). National Competitiveness Report 2016-2017. Bogotá.
OSPINA HERNÁNDEZ, M. (2008). Fluvial navigation in Colombia. Cartagena de Indias.
REPUBLIC OF COLOMBIA (2015). Fluvial master Plan of Colombia. Bogotá, Colombia.