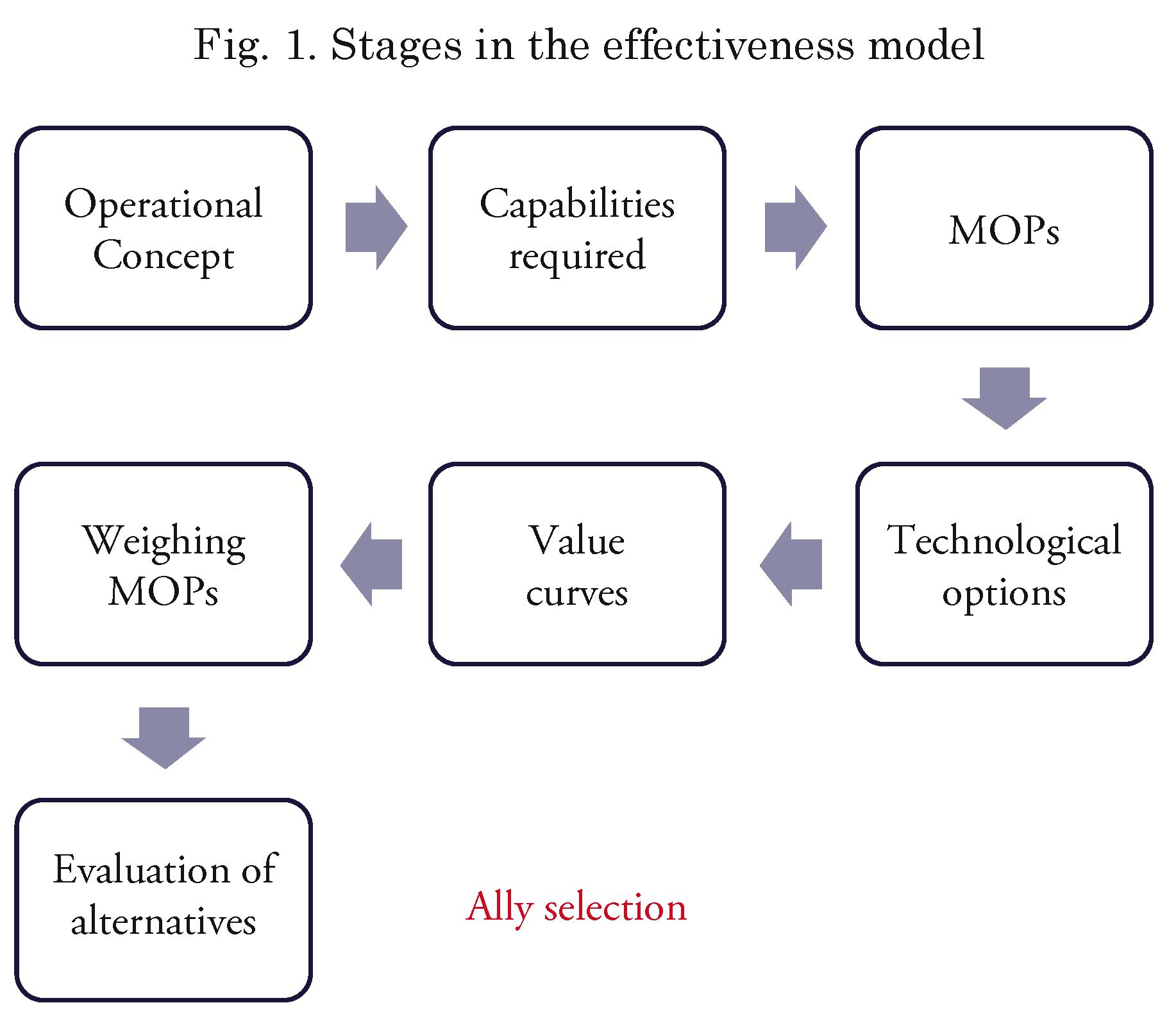
Fig. 1 presents a general view of the different phases of the model, which allows to obtain an Overall Measurement Of Effectiveness (OMOE) [2], which is acquired for each selection alternative. e following premises are required for the development of the project:
-
The operational includes operation, maintenance, and integrated logistic support of the system to be developed.
-
The operational capacities required include the high-level functionalities which must provide the solution and capacities to develop in order to extend the life cycle.
-
The Measures of Performance (MOP), are weighted values of the different capacities and functionalities to be assessed in the model.
-
The technological Options, value curves and weighing of the MOPs are criteria that may be quantifiable according to their nature. These criteria are described in the application of the model.
Risk Assessment Methodology
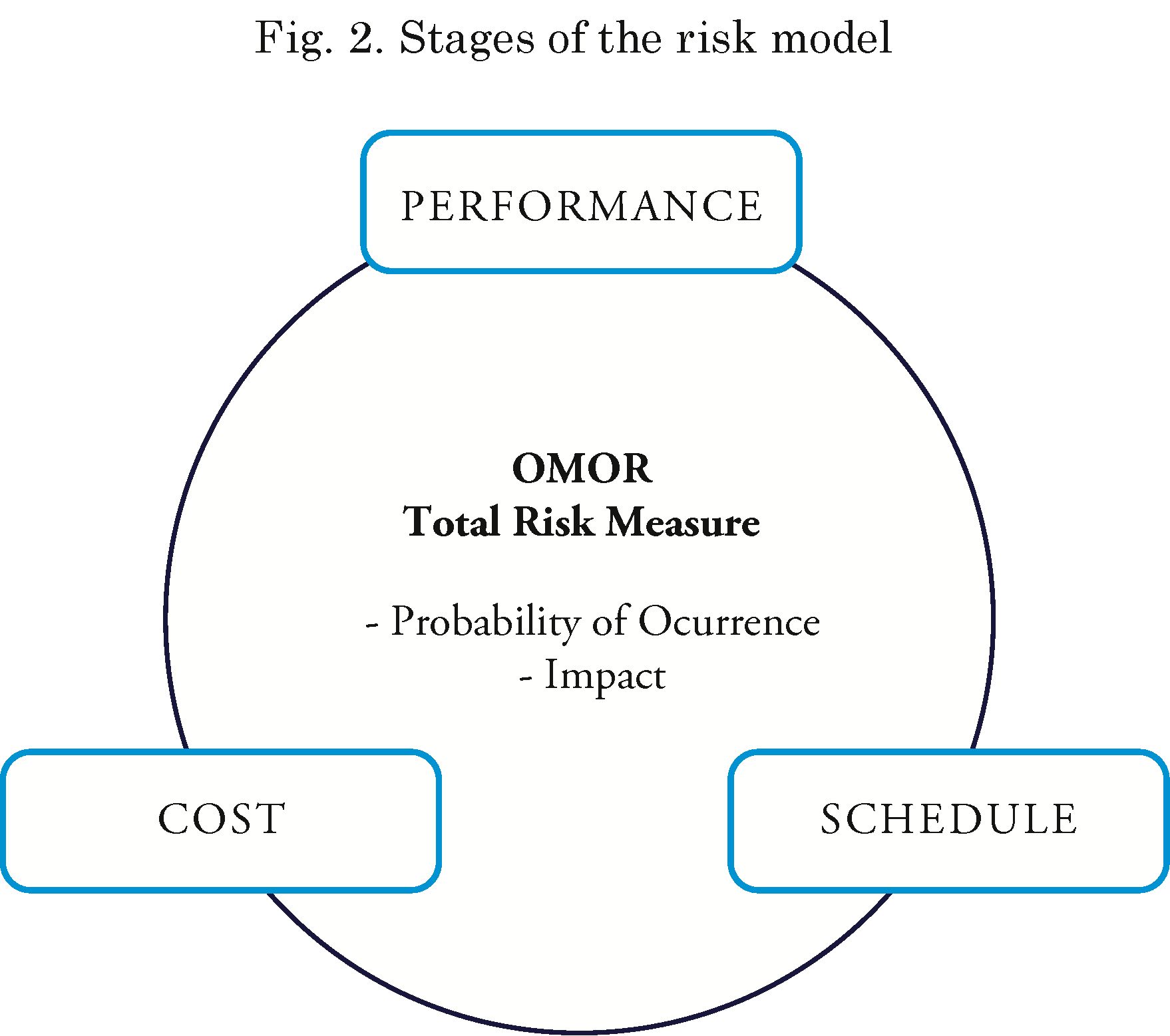
Fig. 2, presents the general outline of risk events, associated to the Overall Measurement of Risk (OMOR). The evaluation of risks associated to performance, cost, and timeline is done through the identification, analysis and priorization of adverse effects to the Project, considering their impact, and occurrence probability.
The development methodology for this model is based on the following procedure:
• Identify potential areas of risk and events associated to each one of them.
• Assign probabilities of Occurrence (Pi) and impacts (Ci) associated to each risk event (Ei).
• Define the function of the Overall Measurement Of Risk (OMOR).
Methodology to evaluate Cost
Fig. 3 shows the general outline of the main components of cost, associated to the Overall Measurement Of Cost (OMOC). The result of this evaluation will show the equivalent value (cost) for each alternative or proposal, including specific costs and additional COTECMAR-ARC costs, associated to each one of the alternatives.
To obtain the OMOC measurement, the costs associated to the development of the system are first identified, which implies the identification of the required association: supplier, ally, or contractor, and inclusion of the required costs for the development of the project (association cost). Likewise, the input (goods) and services, personnel and indirect costs associated to participation (participation costs), required are also related.
Additionally, the costs associated to Integrated Logistic Support, where the costs required to guarantee the life cycle of the system (cost of life cycle) are also identified.

Implementation of the methodology
The following is a description of the model obtained as of the implementation of the methodology presented above.
Effectiveness Model
As of the operational concept, the first Group of experts, identifies the required capacities to achieve success in the execution of the project:
• Functional capacities of the system
• Technical capacities of the system
• Integration capacity of the system
• Capacity to manage the life cycle of the system
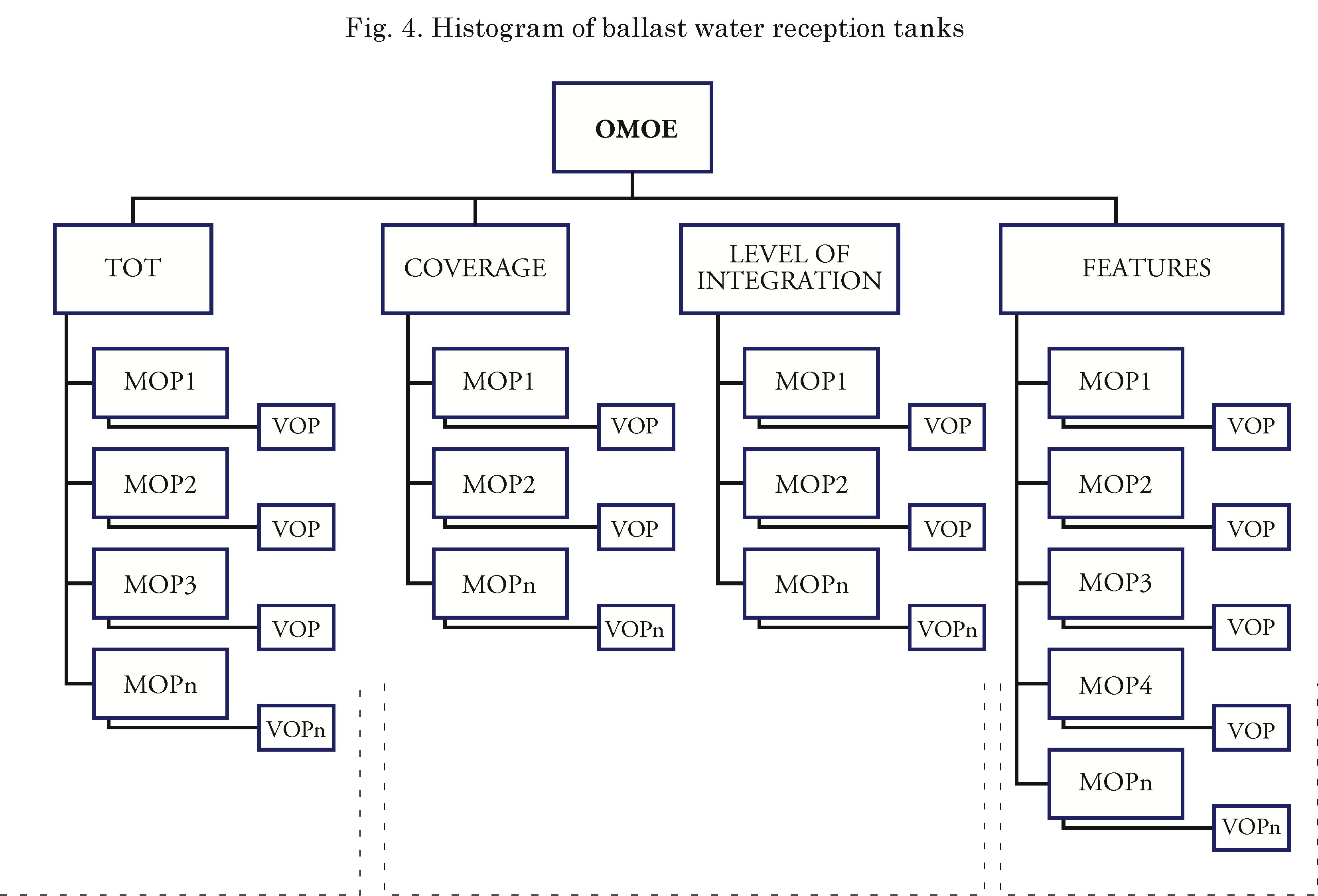
Each one of these categories is associates to an affinity group1 in the assessment model. In this case four (4) groups were identified:
• Technology Transfer (ToT): groups the most significant aspects associated to transfer of knowledge and Know How, which will be evaluated from the proposals.
• System Coverage: groups the aspects associated to the types of units and desired quantities for the system prototypes.
• Integration Level: groups the relevant aspects, associated to the minimum requirements desired for integration and interconnection at a system level and its relation with existing systems in each unit.
• Functionalities: groups aspects associated to function, profit, and operation capacities of the system, per the operational needs of the ARC.
Fig. 4 presents the general outline of the effectiveness model, where the association between affinity groups, the performance measurements and the quantitative measurement of alternatives may be seen. In the same way, the capacities to be obtained by ARC and COTECMAR during the development of the project, may also be seen.
Different MOPs are determined for each affinity model, which are divided into two groups: qualified and quantified. Quantified are those associated to numerical values within the model, while qualified, are those MOPs that are not directly measurable, therefore, making it necessary
____________________________
1 The affinity groups are a set of performance measurements considered to evaluate each one of the alternatives.
to consider options or technological alternatives that may be numerically evaluated and that allow for the evaluation of the presented proposals.
A continuous o discrete value curve is selected for each one of the technological options proposed. Their corresponding superior and inferior limits are suggested for the case of continuous curves and pondérations in the case of discrete curves.
The pondération of the different MOPs is done by the first Group of experts, as of the cross-check of pairs, taking as a reference model the AHP methodology. This weighing allows to identify the level of relevance of a MOP compared to another and to translate this importance into a coefficient or numerical value. This relationship is seen by:
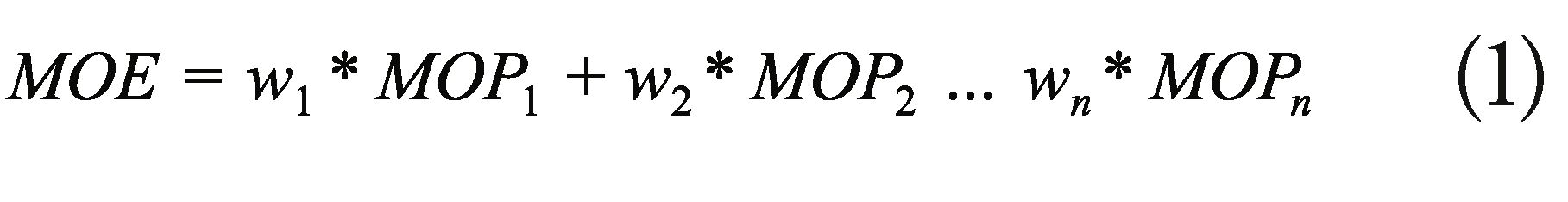
Risk Model
Taking as reference what was established in [3], the different areas of risk stated below are defined:
• Threat
• Requirements
• Design
• Test and evaluation
• Simulation
• Technology
• Logistics
• Production/capacity
• Concurrence
• Capacity of the developer
• Cost of technology/financing
• Schedule/timeline
• Technology management
Although these areas are not the only ones applicable to the type of Project, it is possible to determine similarities among risk events and classify them within them. These events will constitute the aspects to be assessed within the risk model of the Project, considering the performance, timeline and associated costs to the different alternatives. According to [3], the criteria of level of probability of occurrence, Pp, are applied to the levels presented in Table 1.
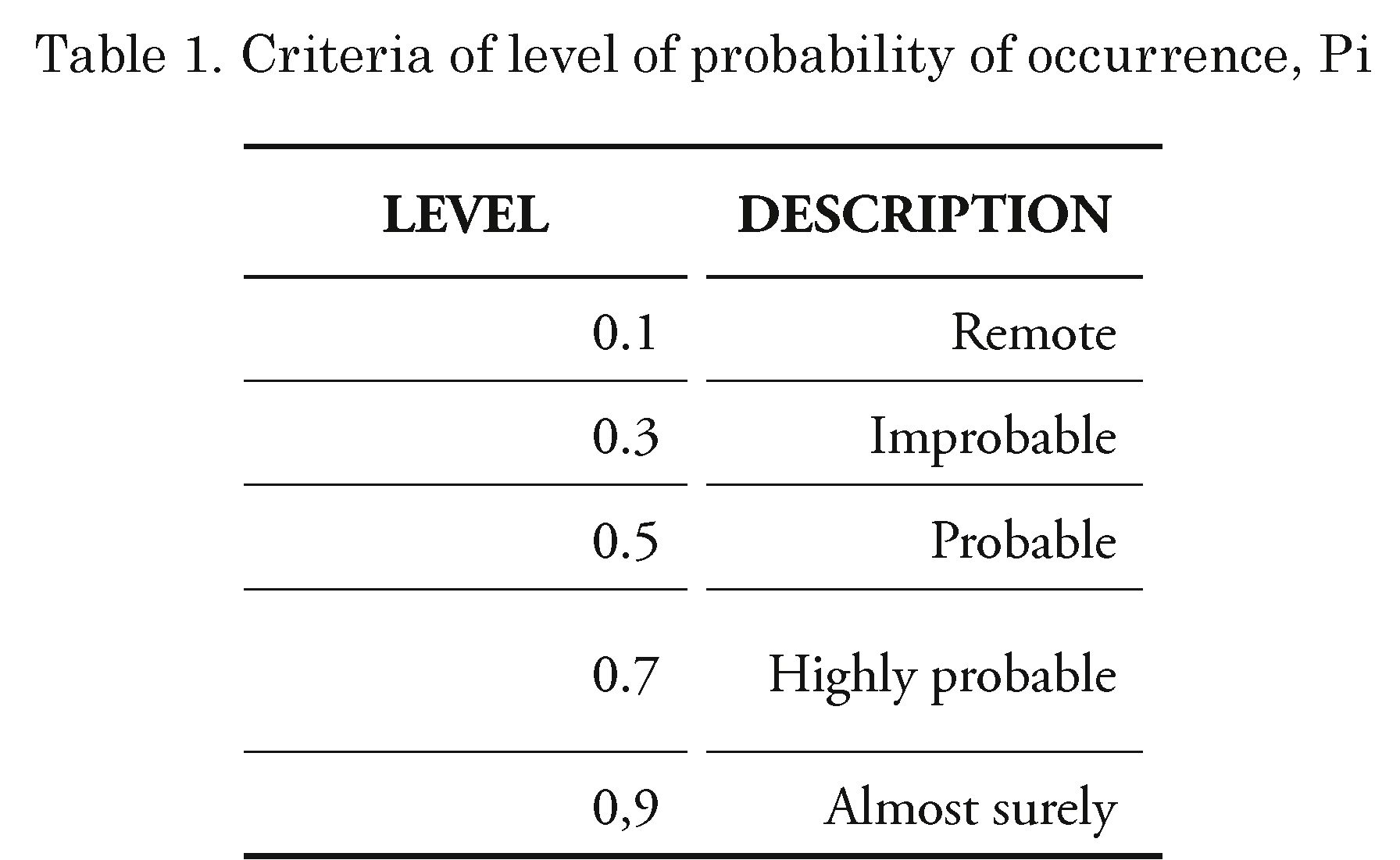
In the same way, the level of impact (C) for each risk event is considered in a scales that varies between 0,1 (minimum) and 0.9 (unacceptable).
Finally, to obtain the OMOR, the values for the MOPs associated to the risks that impact the development of the project are extracted from the effectiveness model. Later, the pairs are compared to obtain a relevance relationship between the risks associated to performance, timeline, and cost. This comparison defines the importance of each one of these three measurements associated to the total measurement of risk, which is finally obtained in function of the following equation 2.

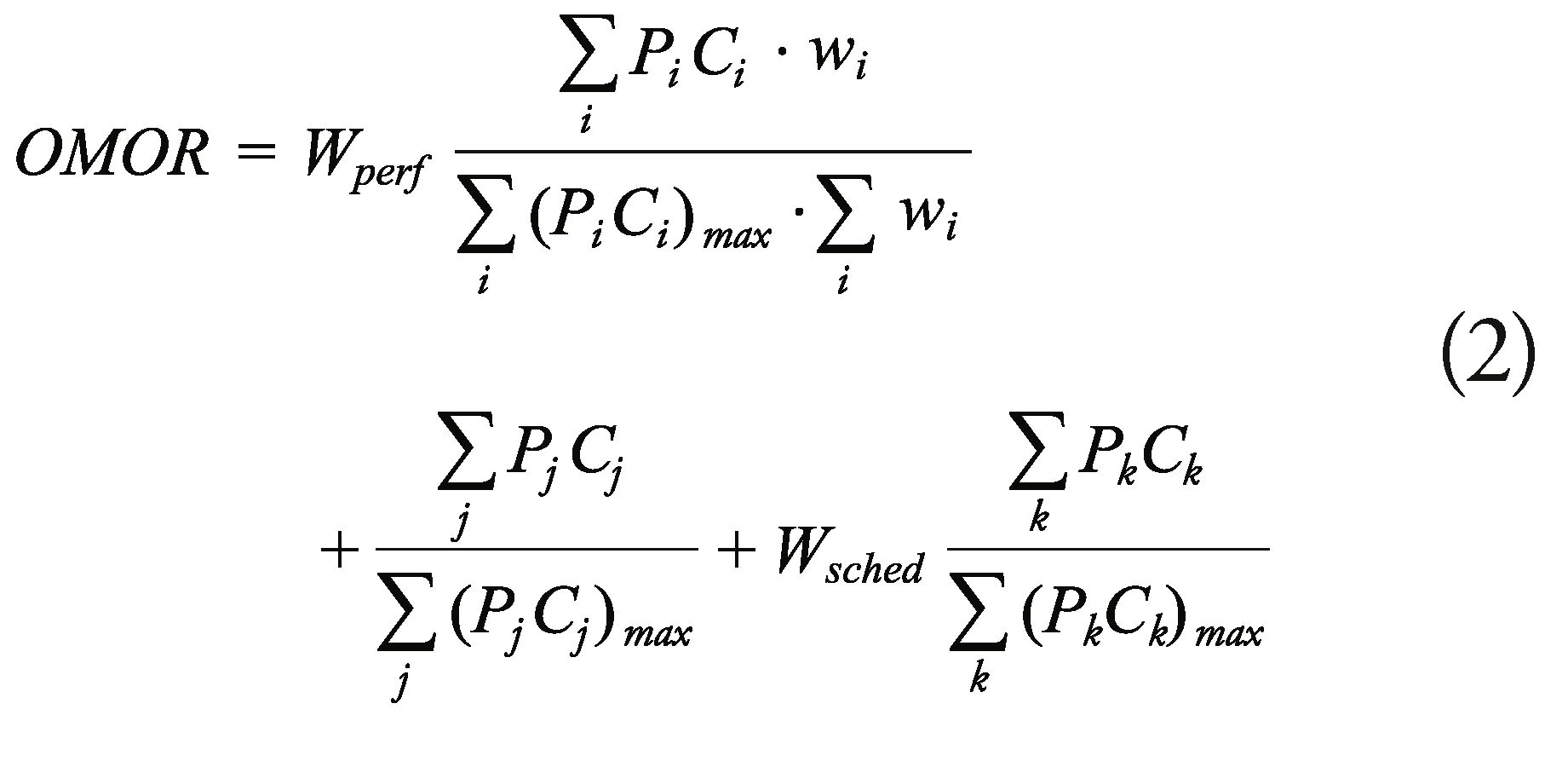
evaluate the costs required by COTECMAR-ARC. This model does not intend to forecast a final cost value for the project, since it is not a cost estimation exercise, however, the activities for each alternative are evaluated according to their associated cost. In the same way, to generate the model, both direct and indirect costs are analyzed and three main levels are established for evaluation:
Association Cost (Ca )
Direct cost of the association required for the development of the Project. Includes the cost related to goods and services, taxes and nationalization.
Cost of participation (Cp)
Direct and indirect costs associated to the contribution of COTECMAR-ARC to fulfill the work schedule, equipment delivery plan, training, on-site work training and development process.
Likewise, the costs associated to the technology transfer process are considered and those that allow for the comparative analysis between the different proposals. An analysis is made for the following costs:
• Personnel:
Associated to the staff that participates in the development activities and transfer of technology. The estimation of this value is done, considering the number of people, number of days and location.

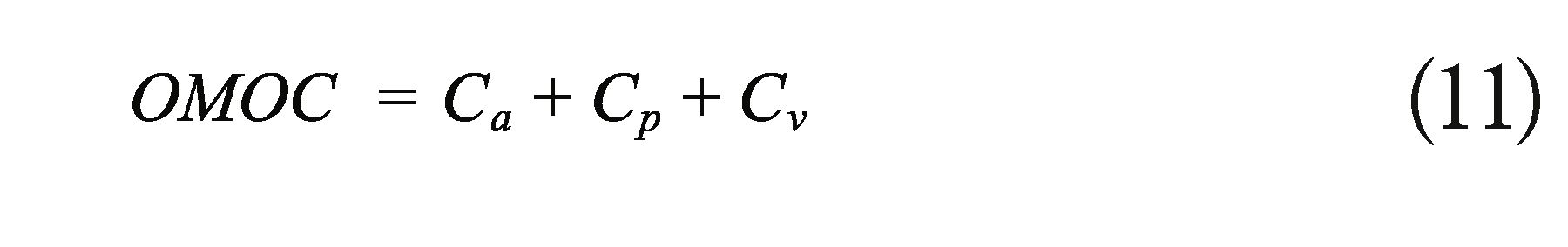
z: factor dependent on the specific number of years (a) and inflation.
The calculation of OMOC is done through the arithmetic addition of each one of the types of costs described:
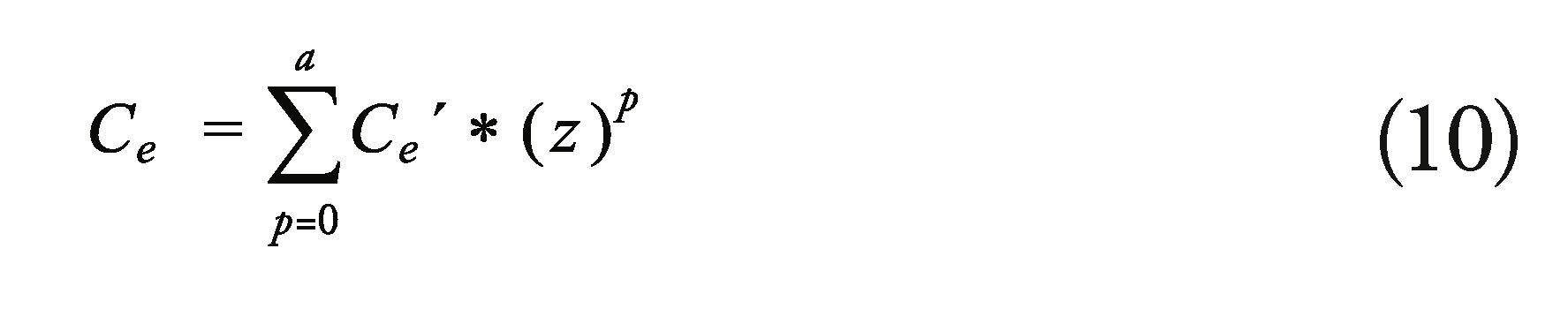
Where:
Q: Acquired Capability to conduct training at the i- est level
/: Number of training levels
This cost is projected to a specific number of years and brought to present value.
The final assessment of this measurement is expressed as follows:
Cost Model
The general measurement for cost or OMOC, is used to analyze the different alternatives and
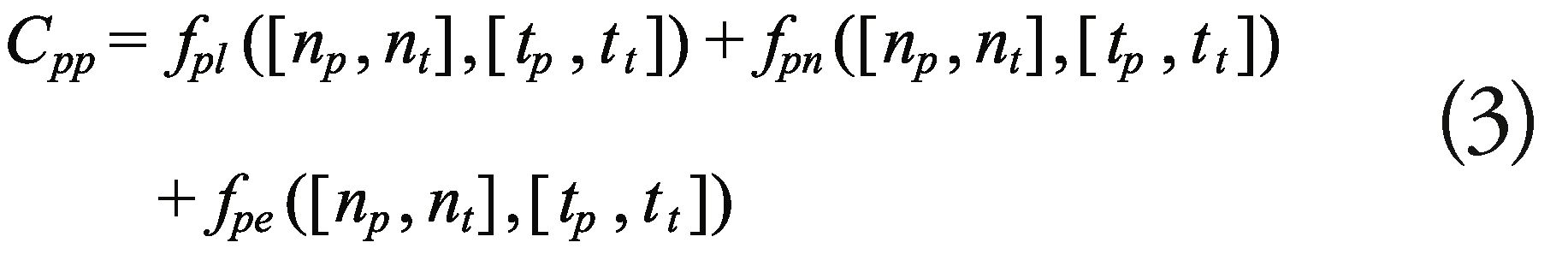
Where:
• Initial training:
Preparation of the staff that participates in the process of technology transfer during the development of a project. To calculate the cost of this training, average market values are used to cover the area of interest.
• Hardware and Software:
Correspond to the use of computer equipment and software during the technology transfer activities.
Cost of life cycle (CJ
Costs projected in time, associated to activities resulting from the process of technology transfer. These costs must be projected along the entire life cycle of the system and represented in present value. The costs associated to the use cycle2 of the naval system to be developed and the maintenance costs (C ) and training costs (C ) are identified as the most relevant to calculate the OMOC. Although this analysis doesn’t only include these cost areas, they are considered the most relevant capacities to acquire through technological transfer and allow to indicate significant changes among the different alternatives.
The cost of life cycle (C ), is expressed as:
z: factor dependent on the number of years (a) and inflation.
Training (CJ:
The level of obtained capabilities is used, by estimating the costs associated to training, in this case, the level of capabilities acquired to render future training throughout the lifecycle of the system, in three different levels of training: basic, intermediate and expert.
For the specific case of the applied project, it is represented by a linear equation of the training costs in function of time/'(¿). This way, the cost of training done by an external agent is expressed as:
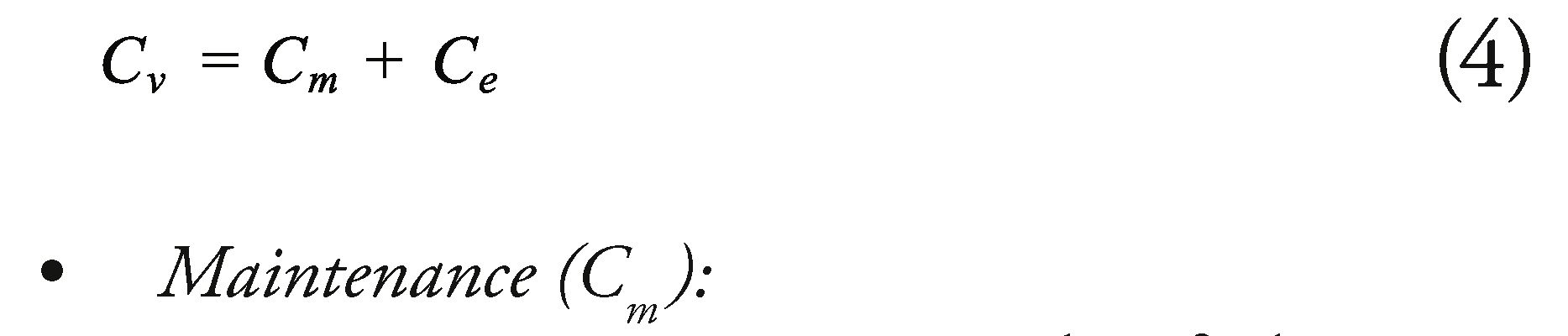
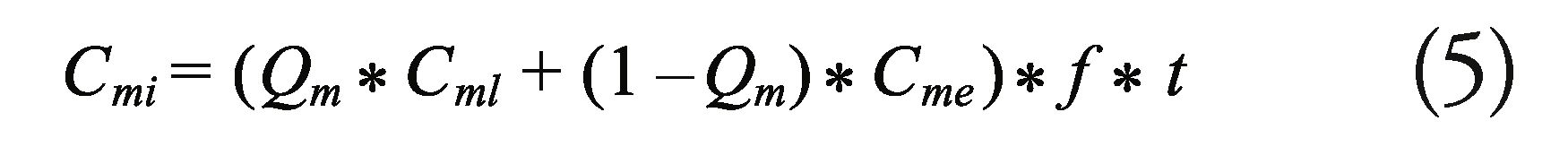
Maintenance activities are classified into 5 different levels according to the degree of intervention in the system and the maintenance classification specified in [5]. The associated cost to each level corresponds to the amount of work hours associated to maintenance activities, frequency for this type of maintenance and vale of hour per person. To assess maintenance, the percentage of capacity is specified from each one of the maintenance levels.
2 Generally, the life cycle of a system may be described in the design, production, commercialization, use and dismantling stages.

This cost, projected to the number of years in the useful lifecycle is transferred to present value, with a profitability equal to the average DTF for the past years, and it is shown in Equation 7.


Application of the model
To obtain the results from the application of the model, five (5) possible scenarios are designed, where each alternative is evaluated and the obtained pondérations are analyzed. Each assessment offers an aid in decision making considering the available budget and the capabilities that COTECMAR-ARC aims to obtain.
Likewise, a desirable range for each one of the measurements of effectiveness, risk and costs is determined, thus filtering the alternatives that do not comply with the following restrictions:
• Effectiveness: obtained value higher than 60%
• Cost: between 20% and 40% of the available Budget for the association.
• At Risk: medium, low and very low risk index.
For the risk index, four ranges are set: Very low
(less than 25%), low (26% - 50%), medium (51% -75%), high (higher than 75%)
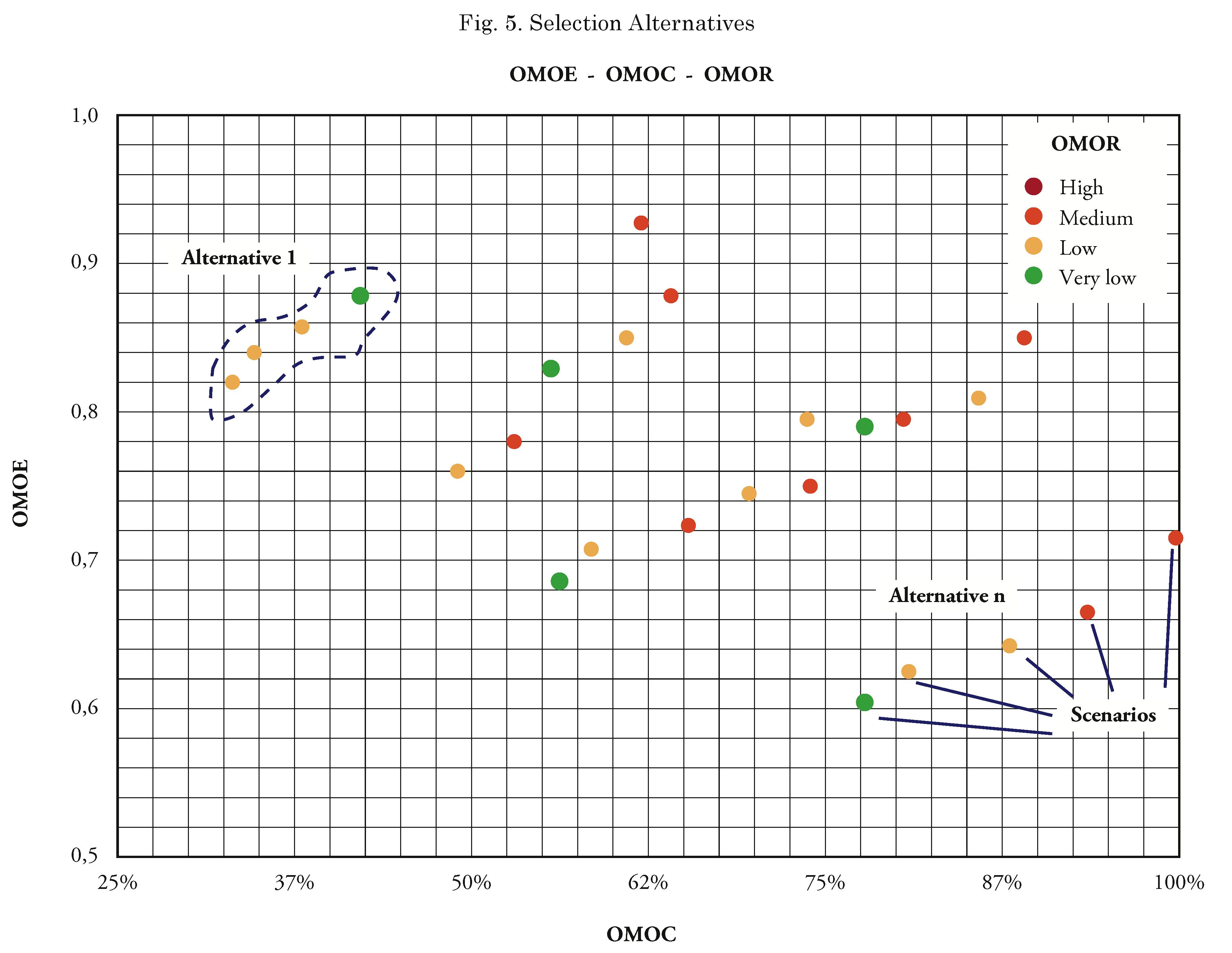
Fig. 5 presents the results of the alternatives assessed in the different proposed scenarios which comply with the established restrictions. The graph shows the effectiveness value in the vertical axis, a cost value in the horizontal axis, provided as a percentage related to the highest cost activity and a risk value represented by a color associated to its pondération.
The highlighted points in the dotted area, show the options that have a higher possibility to be selected because they represent an effectiveness-cost-risk relationship that is favorable and valid to develop the project.
It is noteworthy to state that this model and the results obtained from the assessment, offer great help for decision-making, however, the selection of the alternative is done in function of the analysis of correlation between OMOE, OMOR and OMOC.
Conclusions
The application of the methodology for the design of assessment models presented in this document, results in a reduced Group of alternatives which best adjust to the Budget, risk and desired scope conditions, for the execution of projects, making it easier to make decisions that aim to acquire the capabilities of development of naval systems at ARC-COTECMAR.
The effectiveness, cost, and risk are observed as different attributes that use different measurement units, for which they cannot be rationally combined to produce one sole objective function.
This entails that they are presented individually but simultaneously, in an easily manageable format that allows for interaction between them, easing decision-making.
This format is a space for selection, where the alternatives may be graphed out as points, using the values obtained for effectiveness, cost and risk
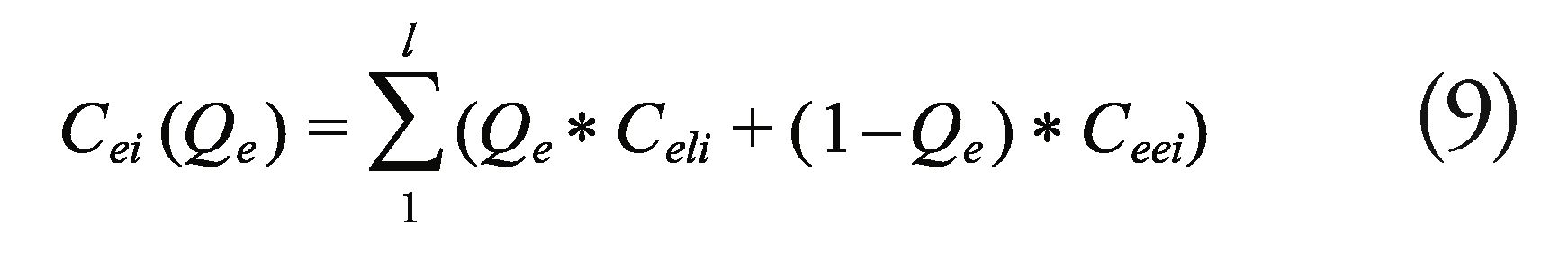
as coordinates, thus offering a perspective that aids at the moment of decision-making.
In general, the methodology proposed by [2] and [3] may be applied to any type of Project, considering the different measures and factors to evaluate, taking into account the risk and cost in the development and the nature of the project.
Bibliographical References
[1] COTECMAR - ARC. Metodología de evaluación para selección del aliado tecnológico. Codesarrollo de un sistema de red táctica naval para la Armada Nacional de Colombia. (Evaluation Methodology For Choosing a Technological Ally) .Cartagena, Colombia. Clasificación: Secreto. Marzo 2015.
[2] J. Carreño, A. Del Gordo, J. Jimenez y O. Tascón. Desarrollo de una Metodología de Soporte para la Toma Racional de Decisiones en la Adquisición de Buques (Development of a Support Methodology for Rational Decision Makingin Ship Acquisition). Bogotá: ESDEGUE- CEM, 2007.
[3] J. Gómez y O. Tascón. “Methodology for analysis and evaluation of alternatives during warship conceptual design”. NEJ vol. 116, pp. 55-72. Abril. 2004.
[4] A. Brown y T. Mierzwicki. “Risk Metric for Multi-Objective Design of Naval Ships”. NEJ vol. 116, pp. 55-72. Abril. 2004.
[5] AFNOR, FD X 60-000, ISSN 0335-3931, Francia, Mayo 2002.