Fatigue Analysis of the Structural Bottom of an Aluminum Planing Craft through Vibratory Load of the Propeller System

Análisis de fatiga del fondo estructural de una lancha planeadora en aluminio por carga vibratoria del sistema propulsor

José R. Marín¹
Carlos A. Cuenca²

Abstract

This work analyzed the structural fatigue of a high-speed craft, which has a propeller system formed by two 493-hp engines connected through speed multipliers to water jet systems. Its aluminum alloy structure has combined-type framing. The useful life of the boat bottom’s structure was determined considering the cyclical loads generated by the propulsion system, using the Finite Elements method and applying the effort-number method of cycles to failure. For this, a structural model was developed of the selected zone, which was analyzed with the SAP2000 program, to obtain complex amplitudes of the stress supported by the structure. Thereafter, with these results the stress range was determined and, then, using S-N curves for Aluminum the number of cycles that needed to be carried out by six structural details selected was determined, for its failure. Using Miner’s Rule, combined with the craft’s assumed work modes, the time of the useful life time of the referential details selected during an hour was determined. Finally, if the craft operates for three hours per day, the bottom structure of the boat analyzed would have a useful life of 14.5 years, when working principally in low speed rating.

Key words: planing craft, fatigue.

Resumen

En este trabajo se analiza la fatiga de la estructura de una lancha rápida, que tiene un sistema propulsor formado por dos motores de 493 hp cada uno, conectados mediante multiplicadores de velocidad a sistemas de chorro de agua. Su estructura de aleación de aluminio tiene cuadernaje de tipo combinado. Se determinó la vida útil de la estructura del fondo de la embarcación, considerando las cargas cíclicas generadas por el sistema de propulsión, utilizando el método de Elementos Finitos y aplicando el método Esfuerzo-Número de ciclos para la falla. Para ello se desarrolló un modelo estructural de la zona seleccionada, el cual es analizado con el programa SAP2000 para obtener las amplitudes complejas de los esfuerzos que soporta la estructura. Luego, con estos resultados se determina el rango de esfuerzos, y posteriormente, usando curvas S-N para aluminio, se determina el número de ciclos que deben desarrollar seis detalles estructurales seleccionados, para su falla. Después, utilizando la regla de Miner, en combinación con modos de trabajo asumidos de la embarcación, se determinó el tiempo de vida útil de los detalles referenciales seleccionados en una hora. Finalmente, si la embarcación operara 3 horas por día, la estructura del fondo de la lancha analizada tendría una vida útil de 14.5 años, cuando trabaja principalmente en régimen de velocidad baja.

Palabras claves: lancha planeadora, fatiga.

Date Received: July 8th, 2014 - Fecha de recepción: 8 de julio de 2014
Date Accepted: August 24th, 2014 - Fecha de aceptación: 24 de agosto de 2014

________________________

1 ESPOL. 1Facultad de Ingeniería Marítima, Ciencias Biológicas, Oceánicas y RR.NN. Guayaquil, Ecuador. e-mail: jrmarin@espol.edu.ec
2 SLEM S.A. Guayaquil, Ecuador. e-mail: ccuenca@espol.edu.ec
............................................................................................................................................................

Introduction

The vibratory forces generated by a ship’s propulsion system can cause a reduction of the resistance of the structural material, a phenomenon known as fatigue (Bannantine, 1990). After a high number of cycles, even with low stress level, cracks that disable the structure may be formed. For planing crafts, given the high power installed, the level of the vibratory excitation forces is quite high and the fatigue produced must be analyzed. This effect is magnified by the presence of stress hot points and weld joints, typical of ship structures. All this may lead to an accelerated process of the appearance of fissures after a given number of cycles.

Due to the prior explanation, emphasis must be made on analyzing the phenomenon of fatigue in high-power crafts to determine the number of cycles after which the formation of cracks on the structure may be expected. For this, classifying societies have processes to determine the useful life time of ship structures, applying the Stress-Useful life method. These societies consider the stress range applied to structural details, along with Miner’s linear damage rule, see ABS (2011) and DNV (2011).

This work sought to analyze the influence of fatigue on the bottom structure of a planing craft subjected to the vibratory action generated by the torque of the main engines and by the thrust generated by the propeller (Cuenca, 2014). Unfortunately, the literature available locally has few references with details on this type of calculation. Thereby, it is expected that these results provide an additional point of reference to compare the classical requirement, creep failure, to this other failure mode, due to fatigue, in case of small, high-speed crafts.

Structural modeling of the boat bottom

Structural model

The craft analyzed has a length of 11 m and was designed to reach a speed of 32 knots, ASTINAVE (2011). It is completely constructed in 5086 aluminum alloy and has a structure with combined-type framing, with ‘L’-type longitudinals with 48-cm separations and ‘L’ type with 75-cm separation. The thickness on the bottom is of 4.76 mm. For its propulsion, it has two 493-hp diesel engines and these, through speed multipliers are joined to water jet systems, which work at 3000 rpm, Hamilton (2007).

Fig. 1 presents a structural plan of the craft analyzed, ASTINAVE (2011).

To reduce the size of the structural model to be developed, a segment was taken from the bottom of the structure corresponding to the engine room, from one side; this is the region where the vibratory sources of interest are found for this analysis. The model represents the primary and secondary structural elements, including the perforations on the shell plating for suction and discharge of the water used to propel the craft. The region of the structure analyzed is 3.5 m long, and its width is equal to the semi-breadth to the chine, corresponding to a distance of 1.9 m. The transom was included to analyze the vibratory stress transmitted by the duct of the propeller system. It has been considered that the presence of the keel would help the vibration generated by a propeller system to be manifested only on said side of the structure.

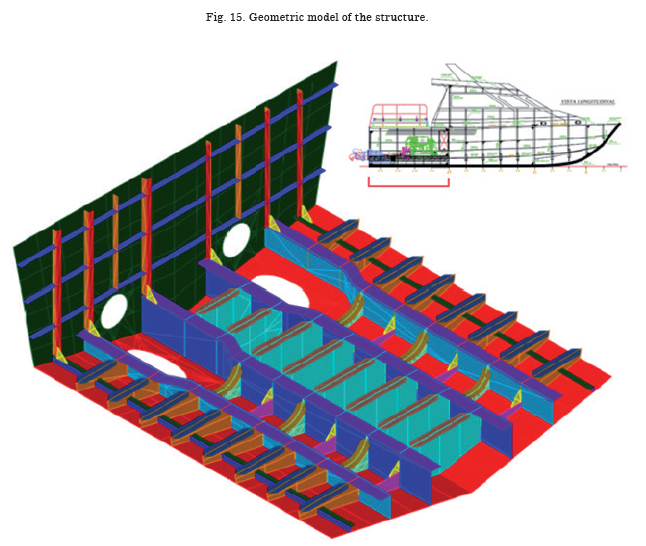
The geometric model is shown in the appendix and served to generate the structural model with MEF, the x axis points in the direction toward the bow, y points toward port, and z points up. In said model, flat areas are defined to then model the shell plating of the bottom and transom, and the reinforcement cores; lines are also defined that will serve to generate, in simplified manner, reinforcement flanges.

The geometric model is imported from the SAP2000 commercial package, where the structural characteristics of the sections and of the material are added (E=7.1E10 N/m2, ν=0.33), taken from the web site: asm.matweb. Finally, simple support boundary conditions are imposed on the model edges. On the centerline plane, upon restricting the rotation in axial direction, high levels of stress were produced, which appeared incorrect, which is why it was decided to impose simple support conditions in said nodes. By restricting the lateral translation (y Global) of various nodes located vertically, a restriction is represented of the rotation in x direction. The characteristics of the structural elements are presented in Table 2.

To represent the inertia of the engine propeller mass, solid elements covering the volume of said equipment are included, and with adequate density to recover its original mass. Besides, to represent the duct of the water jet system, steel beam elements were included, joining the nodes around the perforations of the bottom with those of the transom perforation. Thus, bottom and transom vibrate in phase, as a result of the high rigidity of the propeller duct.

Fig. 3 shows an image of the bottom and the corresponding structural model, as a way of proving their similarity.

Added Mass

The bottom of the boat analyzed, when submerged in water, supports the hydrodynamic effect, denominated added mass, generated by the interaction between the bottom’s vibrating plate and the fl uid in which it is immersed. Th e following formula taken from Korotkin (2009) was used to estimate the added mass per unit of area:

where μ is a parameter that depends on the plate’s aspect ratio, which has dimensions l x b, n is the number of half waves formed by the plate when oscillating, and ρ and ρ₁ are the densities of the fl uids at each side of the plate.

By applying formula (1), the added mass per unit of area is 140 kg/m², considering vibration with a half wave and the interior fl uid’s density as null. By dividing this value for the bottom’s thickness, an “added density” will result that will be added to that of the structural material. Th e resulting value, 32103 kg/m3 is the density included as data for the bottom’s plates. Th is value is quite high and deserves future corroboration.

Typically, for the present analysis was assumed 2% structural dampening, which results from applying the model, available in the structural analysis program used.

Analysis of vibratory stress

Vibratory load to apply

Th e engine room of the craft analyzed has the engine propellers seated on the primary longitudinal reinforcements; also, on said structural elements are the water jet systems, which are attached to the craft’s bottom and transom. Th ese two will be the vibration sources acting directly on the boat’s structure. Th e resulting alternative stresses will aff ect the useful life of the craft’s structure.

Th is work considered the load due to the sixth harmonic of the torque generated by the cylinders, given that they are in phase among each other; the frequency of this harmonic is 3*rpm, given that it is a four-stroke engine. It is also considered that the water jet produces a load due to the variation the thrust has with the ratio frequency of the blades (rotation frequency by the number of blades).

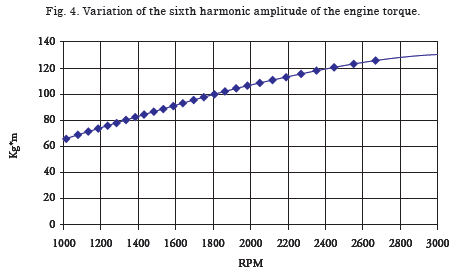
To estimate the amplitude of the oscillating torque, the tangential stress was taken for diff erent values of indicated medium pressure, using the graphics by Moreno (1980). From the eff ective medium pressure, 85% mechanical effi ciency is assumed, to estimate pmi, and assuming quadratic variation with rpm, the tangential stress is calculated for the engine’s diff erent rotation rates. Th e tangential stress multiplied by the area and by the piston stroke produces the vibratory torque. Fig. 4 shows the amplitude of the sixth harmonic of the torque in function of the rotation rate, considering that the harmonics of each cylinder are in phase with each other.

To apply the vibratory moment over the structure, it is considered that the engine is seated on the primary longitudinal reinforcements, which are separated by 0.48 m. An equivalent force is then applied to the ratio of the torque amplitude and the separation between reinforcements, with 180° off set. Th is force is distributed uniformly among the fi ve nodes where said forces are applied, as shown in Fig. 5.

For alternative thrust, it was assumed an amplitude equal to 10% of the mean value developed by each driver, a typical value in the case of open propellers, according to the fi gures published in Long (1992). Th is value is considered representative for the case of conventional propellers. Th e average thrust for diff erent rotation rates is estimated from strength calculations by applying the classic Savitsky method for planing boats, Marín et al (2011); a value of -0.02 is used of the deduction of thrust, t. Given that the system has two propellers, this amplitude was divided by two and, then, by the number of nodes of the connection of the duct with the craft’s bottom and transom. Th e frequency of this excitation corresponds to what is known as the axis blade:rpm ratio for the number of blades of the propeller.

Originally, the plan was to also include as excitation the water pump impeller imbalance. However, according to Long (1992), said load may be in the order of 1% of the propeller’s weight, which results in a low value compared to the other two excitations, and due to this it was discarded.

Selection of structural details to analyze in fatigue

By applying the two excitations to each of their corresponding frequency, then the zones of maximum alternative stress were identified to estimate the operation time necessary for the appearance of cracks due to fatigue. Fig. 7 shows a typical amplitude distribution of normal stress through excitation of the engine’s vibratory torque at a rotation rate of 2600 rpm; in the case shown, the amplitudes of the excitation forces acting on each node are taken as 1 kg and then they are corrected linearly according to the real amplitude of excitation. A similar process was carried out for the excitation due to the vibratory thrust generated by the propeller systems.

Upon obtaining the results of the normal stress distributions and observing where the maximum values are six structural details were selected for fatigue analysis:

• The plate from the bottom between the longitudinal reinforcements, under the engine.

• The main longitudinal reinforcement near the joint between the bottom and the transom.

• The shell plating from the bottom under the side main reinforcement, in the union with discontinuity in direction toward the stern.

• The bottom’s shell plating under the main reinforcement toward the keel, in the joint with the discontinuity in direction toward the stern;

• The shell plating above the duct´s clamping perforation edge on the transom.

• The bottom’s shell plating under the main reinforcement toward the keel, close to the stern.

Table 4 (see pag. 64) presents the different maximum stress zones, when they appear as vibratory torque excitation and the oscillatory thrust.

Calculation of stress in the hot points

In the bottom of the boat analyzed, a structural analysis was performed by applying cyclical loads generated by engine torque and propeller thrust. From these results, it was determined that the highest stress is produced for the cyclic load due to engine torque, in “detail 1”, at a frequency of 107.5

CPS with a value of 47 Kg/cm2. Additionally, it was obtained that, in general, the load due to thrust generates minor stress compared to those obtained due to the load from the engine’s cyclical torque.

Thereafter, the so-called hot-spot stress (HSS) was calculated for the details analyzed, depending on the type of axial or bending load, following the process explained in DNV (2011). Table 5 summarizes the stress range (2*amplitude), for the different details, for both excitations, considering that the craft’s engines operate at different rotation rates.

Note that in spite of increasing the rotation rate the excitation amplitudes grow; the responses do not follow that pattern. This is probably due to the presence of local resonant situations.

Calculation of the useful life of the boat’s bottom

For the fatigue analysis of the structure from the bottom of the boat analyzed, Stress-Life and S-N curves were used for the 5086 aluminum alloy published in the Eurocode (2011). The S-N curves used depend on the type of detail (plate and welded joint), and on the flexural and axial type load to which they are subjected:

Figs. 13 show the evaluations of the number of cycles for the failure, Ni, according to the type of load for each detail. In this study, given the influence of the structure’s operating environment, the second region of the S-N curve is prolonged without limit, that is, a stress limit due to fatigue is not recognized.

With the frequency of each excitation, the number of cycles developed in one hour were estimated, n_i. Then, with the values of the number of cycles for the failure, N_i, previously determined, the contribution of the damage in each detail was estimated with the following relation:

Thereafter, by applying Miner’s rule of cumulative linear damage, Bannantine (1990), the useful life time consumed was determined for each referential detail analyzed. Given that both vibration sources act simultaneously, their life reduction is added:

where i denotes the speed rating considered.

The damage percentage according to equation (3) was calculated for different rpm of the main engine, but the craft does not operate a single speed. Then, due to the lack of information on how to use the propeller installations, three ways to operate the boat were established:

• Navigation principally at low speed,
• Navigation principally at high speed, and
• Uniform navigation at several speeds.

Accumulated damage per hour corresponds to the previous sum, equation (2), but multiplied by the percentage of use, according to the work mode. The inverse of this parameter would correspond to the number of hours of operation it would take to reach failure in each detail; the results are shown in Table 6 (See Pag. 73).

The referential element reduced in greatest percentage in its useful life is detail 1, for work mode 1. Finally, the number of years it would take each structural detail to reach its failure will be estimated.

Useful life of the boat’s bottom

The useful life of the bottom of the boat is analyzed, using the values of total hours until failure for each structural detail calculated for which the boat’s hours of work per year were assumed.

Three cases were taken for this analysis: the boat navigating for three, four, and five hours per day, during the whole year. These represent 1095, 1460, and 1825 hours of operation in one year. Upon conducting this analysis, it was obtained that the boat’s bottom has a useful life restricted by “detail 1”, which corresponds to the bottom’s shell plating, located between the main reinforcements under the main engine, which has a useful life time of 5.4 years, navigating a fourth part of the day, in work mode 1. The inverse of the accumulated damage per hour will correspond to the number of hours to reach failure through fatigue of each structural detail.

The detail that would most rapidly reach failure would be number 1, in work mode 1, that is, operating a longer time at low speed. If the craft operated continuously three hours per day, the failure of detail 1 would occur in 14.5 years.

Conclusions

TThis project determined the useful life of the structural bottom of a planing patrol boat, using the method of Range of Stress-Number of Cycles for the failure, which includes an estimation of stresses, developed through a structural analysis using finite elements. The model analyzed included the structural details found in the zone selected, and the cyclical loads due to the propeller system (engine torque and thrust), and according to that obtained the following is concluded:

It is considered that the structural model developed is suitable, given that it includes all the details with the characteristics shown in the structural plans provided by the manufacturing shipyard. In addition, the aspect ratio of the plate elements used in the discretization is below 3.0, and the element of greater dimension used in the whole numerical model is of 47 x 41 mm. The acting loads were methodically estimated and have been applied in realistic manner in the numerical model.

The stress distributions obtained are acceptable, given their normally continuous behavior in the referential details selected, for both types of loads analyzed in the different excitation frequencies applied.

Miner’s rule of linear accumulated damage was used to determine the number of hours it would take the structural details to fail. With this, it was determined that the boat has a lower useful life for a work mode in which it navigates most of the time at low speeds. Finally, it was determined that detail 1 of the craft analyzed will have a useful life time of 14.5 years navigating three hours per day continuously.

Recommendations

The evaluation of the added mass in the bottom panels produced very high values, leading to recommend experimental works to test said results.

The vibration analyzed is developed at high frequencies, possibly with high local effects; therefore, to confirm the numerical results, it is recommended to measure the vibratory response of the boat’s bottom structure during navigation, or it would be convenient to conduct experiments with models and excitation of the type herein considered.

Finally, it is recommended to also determine real spectra of work modes for these types of crafts.

Acknowledgments

The authors thank ASTINAVE for providing the technical information to carry out this project.

Bibliography

AEROSPACE SPECIFICATION METALS Inc. MatWeb. [Online]. http://asm. matweb.com/ search/SpecificMaterial. asp?bassnum=MA5086H116

AMERICAN BUREAU OF SHIPPING, "Guide for Building and Classifying High-speed Craft". ABS, 2012.

AMERICAN BUREAU OF SHIPPING, "Structural Direct Analysis for High Speed Craft". ABS, 2011.

ASTINAVE E.P., Memoria Técnica de la Lancha Guayas. Guayaquil, 2011.

BANNANTINE, J., COMER, J., and HANDROCK, J., Fundamentals of Metal Fatigue Analysis. Pearson Edition, 1990.

CUENCA, C., Determinación de la Vida Útil del fondo de una embarcación construida en Aluminio por Carga Vibratoria del Sistema Propulsivo. Tesis de Ingeniería Naval, FIMCBOR, ESPOL, Guayaquil, 2014

DET NORSKE VERITAS, Rules for Classification of Speed, Light Craft, and Naval Surface Craft, DNV, 2011.

European Committee for Standardization, Eurocode 9: Design of Aluminium Structures, Brussels, 2011.

HAMILTON JET, Manual de diseño de la serie HJ de Hidrojets, 2007.

KOROTKIN, A., Added Masses of Ship Structures. Springer, 2009.

LONG, CH., Propellers, Shafting, and Shafting System Vibration Analyses, Cap. X en Marine Engineering, Harrington, Ed., SNAME, 1992.

MARÍN, J., MIRANDA, L., and MACAS, F., Análisis de resultados propulsivos en una lancha planeadora de 11 m. Jornadas Técnicas sobre Propulsión de Buques, Colegio de Ingenieros Navales del Ecuador, Guayaquil, 2011.

MORENO, V., Motores de Combustión Interna, Vol. II. Escuela Técnica Superior de Ingenieros Navales, Madrid, 1980.

OTERO, C., Tipología y análisis de fallos en la estructura de los buques mercantes, 2ª parte. Revista Ingeniería Naval, Nov. 2004.

Appendix